Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T17:55:58.706Z Has data issue: false hasContentIssue false
  • English
  • Français

HAUSDORFF DIMENSION OF THE SET APPROXIMATED BY IRRATIONAL ROTATIONS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  14 February 2018

Dong Han Kim ,
Michał Rams  and
Baowei Wang
Dong Han Kim
Affiliation:
Department of Mathematics Education, Dongguk University – Seoul, Seoul 04620, Korea email [email protected]
Michał Rams
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, 00-956 Warszawa, Poland email [email protected]
Baowei Wang
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China email [email protected]
Get access

Abstract

Let 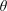$\unicode[STIX]{x1D703}$ be an irrational number and 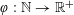$\unicode[STIX]{x1D711}:\mathbb{N}\rightarrow \mathbb{R}^{+}$ be a monotone decreasing function tending to zero. Let

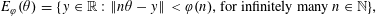$$\begin{eqnarray}E_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D703})=\{y\in \mathbb{R}:\Vert n\unicode[STIX]{x1D703}-y\Vert <\unicode[STIX]{x1D711}(n),\text{for infinitely many }n\in \mathbb{N}\},\end{eqnarray}$$
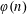i.e. the set of points which are approximated by the irrational rotation with respect to the error function $\unicode[STIX]{x1D711}(n)$. In this article, we give a complete description of the Hausdorff dimension of 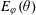$E_{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D703})$ for any monotone function 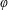$\unicode[STIX]{x1D711}$ and any irrational 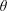$\unicode[STIX]{x1D703}$.

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 11J71: Distribution modulo one 28A80: Fractals
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 267 - 283
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beresnevich, V. and Velani, S., A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) 2006, 971–992.Google Scholar
Bernik, V. I. and Dodson, M. M., Metric Diophantine Approximation on Manifolds (Cambridge Tracts in Mathematics 137 ), Cambridge University Press (Cambridge, 1999).CrossRefGoogle Scholar
Bugeaud, Y., A note on inhomogeneous Diophantine approximation. Glasg. Math. J. 45 2003, 105–110.Google Scholar
Fan, A. and Wu, J., A note on inhomogeneous Diophantine approximation with a general error function. Glasg. Math. J. 48(2) 2006, 187–191.CrossRefGoogle Scholar
Fuchs, M. and Kim, D., On Kurzweil’s 0–1 law in inhomogeneous Diophantine approximation. Acta Arith. 173 2016, 41–57.Google Scholar
Halton, J. H., The distribution of the sequence n𝜉(n = 0, 1, 2, …). Proc. Cambridge Philos. Soc. 61 1965, 665–670.Google Scholar
Kim, D., Refined shrinking target property of rotations. Nonlinearity 27(9) 2014, 1985–1997.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform Distribution of Sequences (Pure and Applied Mathematics), John Wiley & Sons (New York, 1974).Google Scholar
Kurzweil, J., On the metric theory of inhomogeneous Diophantine approximations. Studia Math. 15 1955, 84–112.Google Scholar
Liao, L. and Rams, M., Inhomogeneous Diophantine approximation with general error functions. Acta Arith. 160 2013, 25–35.CrossRefGoogle Scholar
Minkowski, H., Diophantische Approximationen: Eine Einführung in die Zahlentheorie, Chelsea Publishing (New York, 1957).Google Scholar
Schmeling, J. and Troubetzkoy, S., Inhomogeneous Diophantine approximations and angular recurrence for billiards in polygons. Mat. Sb. 194 2003, 129–144.Google Scholar
Tseng, J., On circle rotations and the shrinking target properties. Discrete Contin. Dyn. Syst. 20(4) 2008, 1111–1122.CrossRefGoogle Scholar
Xu, J., Inhomogenous Diophantine approximation and Hausdorff dimension, PhD Thesis, Wuhan University, 2008.Google Scholar