Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:37:30.095Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE

Part of: Additive number theory; partitions Multiplicative number theory

Published online by Cambridge University Press:  25 January 2018

Joni Teräväinen
Joni Teräväinen*
Affiliation:
Department of Mathematics and Statistics, University of Turku, 20014 Turku, Finland email [email protected]
Get access

Abstract

We study the Goldbach problem for primes represented by the polynomial 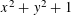$x^{2}+y^{2}+1$. The set of such primes is sparse in the set of all primes, but the infinitude of such primes was established by Linnik. We prove that almost all even integers $n$ satisfying certain necessary local conditions are representable as the sum of two primes of the form 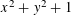$x^{2}+y^{2}+1$. This improves a result of Matomäki, which tells us that almost all even $n$ satisfying a local condition are the sum of one prime of the form 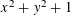$x^{2}+y^{2}+1$ and one generic prime. We also solve the analogous ternary Goldbach problem, stating that every large odd $n$ is the sum of three primes represented by our polynomial. As a byproduct of the proof, we show that the primes of the form 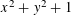$x^{2}+y^{2}+1$ contain infinitely many three-term arithmetic progressions, and that the numbers 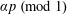$\unicode[STIX]{x1D6FC}p~(\text{mod}~1)$, with $\unicode[STIX]{x1D6FC}$ irrational and 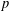$p$ running through primes of the form 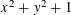$x^{2}+y^{2}+1$, are distributed rather uniformly.

MSC classification

Primary: 11P32: Goldbach-type theorems; other additive questions involving primes
Secondary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values 11N36: Applications of sieve methods
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 20 - 70
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baier, S., A note on Diophantine approximation with Gaussian primes. Preprint, 2016,arXiv:1609.08745 [math.NT].Google Scholar
Friedlander, J. and Iwaniec, H., Opera de Cribro (American Mathematical Society Colloquium Publications 57 ), American Mathematical Society (Providence, RI, 2010).CrossRefGoogle Scholar
Green, B., Roth’s theorem in the primes. Ann. of Math. (2) 161(3) 2005, 1609–1636.CrossRefGoogle Scholar
Green, B. and Tao, T., Restriction theory of the Selberg sieve, with applications. J. Théor. Nombres Bordeaux 18(1) 2006, 147–182.CrossRefGoogle Scholar
Green, B. and Tao, T., The primes contain arbitrarily long arithmetic progressions. Ann. of Math. (2) 167(2) 2008, 481–547.CrossRefGoogle Scholar
Guo, V. Z., Piatetski–Shapiro primes in a Beatty sequence. J. Number Theory 156 2015, 317–330.CrossRefGoogle Scholar
Harman, G., Prime-Detecting Sieves (London Mathematical Society Monographs Series 33 ), Princeton University Press (Princeton, NJ, 2007).Google Scholar
Iwaniec, H., Primes of the type 𝜙(x, y) + A where 𝜙 is a quadratic form. Acta Arith. 21 1972, 203–234.CrossRefGoogle Scholar
Iwaniec, H., The half dimensional sieve. Acta Arith. 29(1) 1976, 69–95.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society Colloquium Publications 53 ), American Mathematical Society (Providence, RI, 2004).Google Scholar
Linnik, J. V., An asymptotic formula in an additive problem of Hardy–Littlewood. Izv. Akad. Nauk SSSR Ser. Mat. 24 1960, 629–706.Google Scholar
Matomäki, K., Prime numbers of the form p = m 2 + n 2 + 1 in short intervals. Acta Arith. 128(2) 2007, 193–200.CrossRefGoogle Scholar
Matomäki, K., The binary Goldbach problem with one prime of the form p = k 2 + l 2 + 1. J. Number Theory 128(5) 2008, 1195–1210.CrossRefGoogle Scholar
Matomäki, K., A Bombieri–Vinogradov type exponential sum result with applications. J. Number Theory 129(9) 2009, 2214–2225.CrossRefGoogle Scholar
Matomäki, K. and Shao, X., Vinogradov’s three primes theorem with almost twin primes. Compos. Math. 153(6) 2017, 1220–1256.CrossRefGoogle Scholar
Mikawa, H., On exponential sums over primes in arithmetic progressions. Tsukuba J. Math. 24(2) 2000, 351–360.CrossRefGoogle Scholar
Montgomery, H. L., Ten Lectures on the Interface between Analytic Number Theory and Harmonic Analysis (CBMS Regional Conference Series in Mathematics 84 ), American Mathematical Society (Providence, RI, 1994). Published for the Conference Board of the Mathematical Sciences, Washington, DC.CrossRefGoogle Scholar
Ramaré, O. and Ruzsa, I. Z., Additive properties of dense subsets of sifted sequences. J. Théor. Nombres Bordeaux 13(2) 2001, 559–581.CrossRefGoogle Scholar
Shi, S.-Y., On the distribution of 𝛼p modulo one for primes p of a special form. Osaka J. Math. 49(4) 2012, 993–1004.Google Scholar
Tolev, D. I., Arithmetic progressions of prime-almost-prime twins. Acta Arith. 88(1) 1999, 67–98.CrossRefGoogle Scholar
Tolev, D. I., The binary Goldbach problem with arithmetic weights attached to one of the variables. Acta Arith. 142(2) 2010, 169–178.CrossRefGoogle Scholar
Tolev, D. I., The ternary Goldbach problem with arithmetic weights attached to two of the variables. J. Number Theory 130(2) 2010, 439–457.CrossRefGoogle Scholar
Wirsing, E., Das asymptotische Verhalten von Summen über multiplikative Funktionen. Math. Ann. 143 1961, 75–102.CrossRefGoogle Scholar
Wu, J., Primes of the form p = 1 + m 2 + n 2 in short intervals. Proc. Amer. Math. Soc. 126(1) 1998, 1–8.CrossRefGoogle Scholar