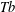Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T01:42:14.891Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERALIZED LOCAL $\mathit{Tb}$ THEOREMS FOR SQUARE FUNCTIONS

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  25 July 2016

Ana Grau De La Herrán  and
Steve Hofmann
Ana Grau De La Herrán
Affiliation:
Department of Mathematics and Statistics, University of Helsinki, Finland email [email protected]
Steve Hofmann
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MI 65211, U.S.A. email [email protected]
Get access

Abstract

A local 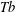$\mathit{Tb}$ theorem is an 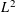$L^{2}$ boundedness criterion by which the question of the global behavior of an operator is reduced to its local behavior, acting on a family of test functions 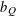$b_{Q}$ indexed by the dyadic cubes. We present two versions of such results, in particular, treating square function operators whose kernels do not satisfy the standard Littlewood–Paley pointwise estimates. As an application of one version of the local 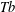$\mathit{Tb}$ theorem, we show how the solvability of the Kato problem (which was implicitly based on local 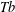$\mathit{Tb}$ theory) may be deduced from this general criterion.

MSC classification

Primary: 42B25: Maximal functions, Littlewood-Paley theory
Secondary: 42B37: Harmonic analysis and PDE
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 1 - 28
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfonseca, M. A., Auscher, P., Axelsson, A., Hofmann, S. and Kim, S., Analyticity of layer potentials and L 2 solvability of boundary value problems for divergence form elliptic equations with complex L ∞ coefficients. Adv. Math. 226 2011, 4533–4606.Google Scholar
Auscher, P., Hofmann, S., Lacey, M., McIntosh, A. and Tchamitchian, P., The solution of the Kato square root problem for second order elliptic operators on ℝ n . Ann. of Math. (2) 156 2002, 633–654.Google Scholar
Auscher, P., Hofmann, S., Muscalu, C., Tao, T. and Thiele, C., Carleson measures, trees, extrapolation, and T (b) theorems. Publ. Mat. 46(2) 2002, 257–325.CrossRefGoogle Scholar
Auscher, P. and Routin, E., Local Tb theorems and Hardy inequalities. J. Geom. Anal. 13 2013, 303–374.Google Scholar
Auscher, P. and Tchamitchian, P., Square Root Problem for Divergence Operators and Related Topics (Astérisque 249 ), Société Mathématique de France (1998).Google Scholar
Auscher, P. and Yang, Q. X., BCR algorithm and the T (b) theorem. Publ. Mat. 53(1) 2009, 179–196.Google Scholar
Christ, M., A T (b) theorem with remarks on analytic capacity and the Cauchy integral. Colloq. Math. LX–LXI 1990, 601–628.Google Scholar
Christ, M. and Journé, J.-L., Polynomial growth estimates for multilinear singular integral operators. Acta Math. 159(1–2) 1987, 51–80.CrossRefGoogle Scholar
Cruz-Uribe, D., Martell, J. M and Pérez, C., Weights, Extrapolation and the Theory of Rubio de Francia (Operator Theory: Advances and Applications 215 ), Birkhäuser/Springer (Basel, 2011).CrossRefGoogle Scholar
David, G., Journé, J.-L. and Semmes, S., Opérateurs de Calderón–Zygmund, fonctions para-accrétives et interpolation. Rev. Mat. Iberoam. 1 1985, 1–56.CrossRefGoogle Scholar
Duoandikoetxea, J. and Rubio de Francia, J. L., Maximal and singular integral operators via Fourier transform estimates. Invent. Math. 84 1986, 541–561.CrossRefGoogle Scholar
Grau de la Herrán, A. and Hofmann, S., A local Tb theorem with vector-valued testing functions. In Some Topics in Harmonic Analysis and Applications (special volume in honor of Shanzhen Lu) (Advanced Lectures in Mathematics 34 ) (eds Li, J., Li, X. and Lu, G.), International Press (Boston, MA, 2016).Google Scholar
Grau de la Herrán, A. and Mourgoglou, M., A Tb theorem for square functions in domains with Ahlfors–David regular boundaries. J. Geom. Anal. 24 2014, 1619–1640.CrossRefGoogle Scholar
Hofmann, S., Local $\mathit{Tb}$ theorems for square functions and application in PDE. Proc. ICM (Madrid, 2006).Google Scholar
Hofmann, S., A proof of the local $\mathit{Tb}$ theorem for standard Calderon–Zygmund operators. Preprint, 2007, arXiv:0705.0840.2.Google Scholar
Hofmann, S., A local Tb theorem for square functions. In Perspectives in Partial Differential Equations, Harmonic Analysis and Applications (Proceedings of Symposia in Pure Mathematics 79 ), American Mathematical Society (Providence, RI, 2008), 175–185.Google Scholar
Hofmann, S., Local T (b) theorems and application in PDE. In Harmonic Analysis and Partial Differential Equations 29–52 (Contemporary Mathematics 505 ), American Mathematical Society (Providence, RI, 2010).Google Scholar
Hofmann, S., Lacey, M. and McIntosh, A., The solution of the Kato problem for divergence form elliptic operators with Gaussian heat kernel bounds. Ann. of Math. (2) 156 2002, 623–631.Google Scholar
Hofmann, S. and Martell, J. M., Uniform rectifiability and harmonic measure I: uniform rectifiability implies Poisson kernels in L p . Ann. Sci. Éc. Norm. Supér. 47 2014, 577–654.CrossRefGoogle Scholar
Hofmann, S., Martell, J. M. and Uriarte-Tuero, I., Uniform rectifiability and harmonic measure II: Poisson kernels in L p imply uniform rectfiability. Duke Math. J. 163 2014, 1601–1654.CrossRefGoogle Scholar
Hofmann, S. and McIntosh, A., The solution of the Kato problem in two dimensions. Proc. Conf. Harmonic Analysis and PDE (El Escorial, Spain, July 2000, Publ. Mat. extra volume (2002), 143–160.CrossRefGoogle Scholar
Hofmann, S. and McIntosh, A., Boundedness and applications of singular integrals and square functions: a survey. Bull. Math. Sci. 1 2011, 201–244.Google Scholar
Hytönen, T. and Martikainen, H., On general local Tb theorems. Trans. Amer. Math. Soc. 364 2012, 4819–4846.Google Scholar
Hytönen, T. and Nazarov, F., The local $\mathit{Tb}$ theorem with rough test functions. Preprint, 2012, arXiv:1206.0907.Google Scholar
Lacey, M. and Martikainen, H., Local Tb theorem with L2 testing conditions and general measures: Calderón–Zygmund operators. Ann. Sci. Éc. Norm. Supér. 49 2016, 57–86.Google Scholar
Lacey, M. and Martikainen, H., Local Tb theorem with L2 testing conditions and general measures: square functions. J. Anal. Math. (to appear), arXiv:1308.4571.Google Scholar
Martikainen, H. and Mourgoglou, M., Boundedness of non-homogeneous square functions and L q type testing conditions with q in (1, 2). Math. Res. Lett. 22 2015, 1417–1457.Google Scholar
McIntosh, A. and Meyer, Y., Algèbres dopérateurs définis par des intégrales singulières. C. R. Acad. Sci. Paris 301(1) 1985, 395–397.Google Scholar
Meyers, N. G., An L p estimate for the gradient of solutions of second order elliptic divergence equations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 17 1963, 189–206.Google Scholar
Nazarov, F., Treil, S. and Volberg, A., Accretive system Tb -theorems on nonhomogeneous spaces. Duke Math. J. 113(2) 2002, 259–312.Google Scholar
Semmes, S., Square function estimates and the T (b) theorem. Proc. Amer. Math. Soc. 110(3) 1990, 721–726.Google Scholar
Stein, E. M. and Weiss, G., Interpolation of operators with change of measures. Trans. Amer. Math. Soc. 87 1958, 159–172.CrossRefGoogle Scholar
Tan, C. and Yan, L., Local Tb theorem on spaces of homogeneous type. Z. Anal. Anwend. 28(3) 2009, 333–347.Google Scholar