Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:14:55.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Fredholm formulae and the Riesz-theory—a base for the null space of I— λoK

Published online by Cambridge University Press:  26 February 2010

Anthony F. Ruston
Anthony F. Ruston
Affiliation:
School of Mathematics and Computer Science, University College of North Wales (Coleg Prifysgol Gogledd Cymru), Deimiol RoadBangor, Caernarvonshire, Wales, LL57 2UW.
Get access

Extract

In an earlier paper [10], I presented a base for the kernel, 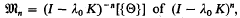and in particular for the null space 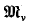of I - λo K ((p.39). I remarked then that the base did not quite correspond to the arrangement given by Zaanen (cf. [13; p. 280], [14; pp. 339, 342]). The purpose of the present paper is to present an alternative base which does correspond to Zaanen's arrangement.

Type
Research Article
Information
Mathematika , Volume 19 , Issue 2 , December 1972 , pp. 213 - 220
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Deprit, André, “Endomorphismes de Riesz”, Ann. Soc. Sci. Bruxelles, Sér. I, 70 (1956), 165–184.Google Scholar
2.Eells, James “A setting for global analysis”, Bull. American Math. Soc. 72 (1966), 751–807.Google Scholar
3.Goldberg, Seymour, Unbounded Linear Operators (McGraw-Hill, 1966).Google Scholar
4.Palais, Richard S., et al, Seminar on the Atiyah-Singer Index Theorem (Annals of Mathematics Studies No. 57, Princeton University Press, 1965).Google Scholar
5.Riesz, Friedrich, “Über lineare Funktionalgleichungen”, Ada Math. 41 (1916), 71–98. Reprinted in Oeuvres Complétes, pp. 1053–1080.Google Scholar
6.Ruston, A. F. “On the Fredholm theory of integral equations for operators belonging to the trace class of a general Banach space”, Proc. London Math. Soc. (2) 53 (1951), 109–124.CrossRefGoogle Scholar
7.Ruston, A. F. “Direct products of Banach spaces and linear functional equations”, Proc. London Math. Soc. (3) 1 (1951), 327–384.CrossRefGoogle Scholar
8.Ruston, A. F. “Formulae of Fredholm type for compact linear operators on a general Banach space”, Proc. London Math. Soc. (3) 3 (1953), 368–377.CrossRefGoogle Scholar
9.Ruston, A. F. “Operators with a Fredholm theory”, Journal London Math. Soc. (1) 29 (1954) 318–326.CrossRefGoogle Scholar
10.Ruston, A. F. “Fredholm formulae and the Riesz theory”, Compositio Math. 18 (1967), 25–48.Google Scholar
11.Ruston, A. F. “Asymptotically quasi-compact products of bounded linear operators”, Journal Austral. Math. Soc. 16 (1973), in the press.CrossRefGoogle Scholar
12.Schechter, Martin, Principles of Functional Analysis (Academic Press, 1971).Google Scholar
13.Zaanen, A. C. “On linear functional equations”, Nieuw Arch. Wiskunde (2) 22 (1948), 269–289.Google Scholar
14.Zaanen, Adriaan Cornelius, Linear Analysis (North-Holland Publishing Co., Amsterdam, 1953).Google Scholar