Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T15:16:17.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier transforms and descriptive set theory

Part of: Connections with other structures, applications

Published online by Cambridge University Press:  26 February 2010

R. Kaufman
R. Kaufman
Affiliation:
Department of Mathematics, University of Illinois, 273 Altgeld Hall, 1409, West Green Street, Urbana, Illinois, 61801, U.S.A.
Get access

Extract

We state some definitions belonging to the two halves of the title, going far enough to state our main results.

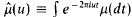Fourier transforms. Let μ be a finite, complex-valued measure on R and its Fourier-Stieltjes transform. We define ℛ to be the set of μ with 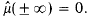When μ ∈ ℛ and φ is of class 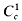(continuously differentiable of compact support), the identity 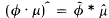shows that θ · μ ∈ ℛ.

MSC classification

Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Research Article
Information
Mathematika , Volume 31 , Issue 2 , December 1984 , pp. 336 - 339
Copyright
Copyright © University College London 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Engelking, R.. General topology (PWN, Warsaw, 1977).Google Scholar
2.Kaufman, R.. Bernoulli convolutions and differentiable functions. Trans. Amer. Math. Soc, 217 (1976), 99–104.CrossRefGoogle Scholar
3.Kaufman, R.. On Bernoulli convolutions. Conference in modern analysis and probability (New Haven, 1982). Contemporary mathematics 26 (Amer. Math. Soc, 1984).Google Scholar
4.Kaufman, R.. Representation of Suslin sets by operators. Manuscript in preparation.Google Scholar
5.Kuratowski, C.. Topologie I, 3rd edition (PWN, Warsaw, 1952). English edition (Academic Press, 1968).Google Scholar
6.Mazurkiewicz, S. et Sierpiński, W.. Sur un probleme concernant les fonctions continues. Fund. Math. 6 (1924), 161–169. Also in W. Sierpinski, Oeuvres Choisies, Vol. II, 559-566 (PWN, Warsaw, 1975).CrossRefGoogle Scholar
7.Zygmund, A.. Trigonometric series II (Cambridge University Press, 1959 and 1968).Google Scholar