Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T21:51:28.627Z Has data issue: false hasContentIssue false
  • English
  • Français

FORMS OF DIFFERING DEGREES OVER NUMBER FIELDS

Part of: Additive number theory; partitions Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  26 September 2016

Christopher Frei  and
Manfred Madritsch
Christopher Frei
Affiliation:
Technische Universität Graz, Institut für Analysis und Computational Number Theory, Steyrergasse 30/II, A-8010 Graz, Austria email [email protected]
Manfred Madritsch
Affiliation:
Université de Lorraine, Institut Elie Cartan de Lorraine, UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France CNRS, Institut Elie Cartan de Lorraine, UMR 7502, Vandoeuvre-lès-Nancy, F-54506, France email [email protected]
Get access

Abstract

Consider a system of polynomials in many variables over the ring of integers of a number field 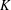$K$. We prove an asymptotic formula for the number of integral zeros of this system in homogeneously expanding boxes. As a consequence, any smooth and geometrically integral variety 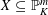$X\subseteq \mathbb{P}_{K}^{m}$ satisfies the Hasse principle, weak approximation, and the Manin–Peyre conjecture if only its dimension is large enough compared to its degree. This generalizes work of Skinner, who considered the case where all polynomials have the same degree, and recent work of Browning and Heath-Brown, who considered the case where 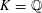$K=\mathbb{Q}$. Our main tool is Skinner’s number field version of the Hardy–Littlewood circle method. As a by-product, we point out and correct an error in Skinner’s treatment of the singular integral.

MSC classification

Primary: 11G35: Varieties over global fields
Secondary: 11P55: Applications of the Hardy-Littlewood method 14G05: Rational points
Type
Research Article
Information
Mathematika , Volume 63 , Issue 1 , 2017 , pp. 92 - 123
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birch, B. J., Forms in many variables. Proc. R. Soc. Lond. Ser. A 265 1961–1962, 245–263.Google Scholar
Browning, T. D. and Heath-Brown, D. R., Forms in many variables and differing degrees. J. Eur. Math. Soc. (to appear). Preprint, 2015, arXiv:1403.5937.Google Scholar
Browning, T. D. and Vishe, P., Cubic hypersurfaces and a version of the circle method for number fields. Duke Math. J. 163(10) 2014, 1825–1883.CrossRefGoogle Scholar
Franke, J., Manin, Yu. I. and Tschinkel, Yu., Rational points of bounded height on Fano varieties. Invent. Math. 95(2) 1989, 421–435.CrossRefGoogle Scholar
Frei, C. and Pieropan, M., O-minimality on twisted universal torsors and Manin’s conjecture over number fields. Ann. Sci. Éc. Norm. Supér. (to appear).Google Scholar
Loughran, D., Rational points of bounded height and the Weil restriction. Israel J. Math. 210(1) 2015, 47–79.Google Scholar
Peyre, E., Hauteurs et mesures de Tamagawa sur les variétés de Fano. Duke Math. J. 79(1) 1995, 101–218.Google Scholar
Schindler, D. and Skorobogatov, A., Norms as products of linear polynomials. J. Lond. Math. Soc. (2) 89(2) 2014, 559–580.Google Scholar
Schmidt, W. M., The density of integer points on homogeneous varieties. Acta Math. 154(3–4) 1985, 243–296.Google Scholar
Skinner, C. M., Rational points on nonsingular cubic hypersurfaces. Duke Math. J. 75(2) 1994, 409–466.Google Scholar
Skinner, C. M., Forms over number fields and weak approximation. Compos. Math. 106(1) 1997, 11–29.CrossRefGoogle Scholar