Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:02:57.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of compact sets and their universals

Part of: Connections with other structures, applications

Published online by Cambridge University Press:  26 February 2010

A. J. Ostaszewski
A. J. Ostaszewski
Affiliation:
Mathematics Department, The University, Leicester LEI 7RH.
Get access

Extract

§1. Introduction and Summary. Throughout X is a complete separable metric space. We write K1 for the family of non-empty compact subsets of X. K1 may be endowed with a metric (first introduced by Hausdorff) under which K1 is complete and separable. We shall make use of the subbase for this metrizable topology of K1 given by sets of the two forms

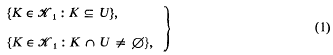
for U open in X (see Kuratowski [4] or E. Michael [9] for a discussion of topologies on the space of subsets of X). if 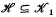we shall be concerned with sets in [0, 1] × X which are universal for ℋ. To define these let us make the convention that, for D ⊆ [0, 1] × X, we write

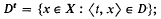
D is said to be universal for ℋ if

MSC classification

Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets)
Type
Research Article
Information
Mathematika , Volume 21 , Issue 1 , June 1974 , pp. 116 - 127
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davies, R. O.. “Sion-Sjerve measures are of Hausdorff type”, J. London Math. Soc. (2), 5 (1972), 526é528.CrossRefGoogle Scholar
2.Frolik, Z.. “A survey of separable descriptive theory of sets and spaces”, Czech. Math. J., 20 (95), 1970, 406–467.CrossRefGoogle Scholar
3.Hurewicz, W.. “Zur theorie der analytischen Mengen”, Fund. Math., 15 (1930), 4–17.CrossRefGoogle Scholar
4.Kuratowski, K.. Topology, Vol. II (Academic Press, 1966).Google Scholar
5.Kuratowski, K. and Szpilrajn, E.. “Sur les cribles fermés et leurs applications”, Fund. Math., 18 (1932), 160–170.CrossRefGoogle Scholar
6.Larman, D. G.. “Projecting and uniformizing Borel sets with. Kσ -sections”, Mathematika, 19 (1972), 231–244.CrossRefGoogle Scholar
7.Larman, D. G. and Rogers, C. A.. “On the descriptive character of certain universal sets” Proc. London Math. Soc, 27 (1973), 385–401.CrossRefGoogle Scholar
8.Ljapunow, A. A., Stschegolkow, E. A., Arsenin, W. J. and Ljapunow, A. A.. Arbeiten zur deskrip-tiven Mengenlehre (Berlin, VEB Deutscher Verlag der Wissenschaften, 1955).Google Scholar
9.Michael, E.. “Topologies on spaces of subsets” Trans. Amer. Math. Soc, 71 (1951), 152–182.CrossRefGoogle Scholar
10.Moschovakis, Y.. “Uniformization in a playful universe” Bull. Amer. Math. Soc, 77 (1970), 731–736.CrossRefGoogle Scholar
11.Ostaszewski, A. J.. On descriptive set theory in Hausdorff spaces, Ph.D. Thesis (London, 1973), Chapter 4.Google Scholar
12.Rogers, C. A.. Hausdorff Measures (Cambridge University Press, 1970).Google Scholar
13.Sierpiriski, W.. General Topology (University of Toronto Press, 1952).CrossRefGoogle Scholar