Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:05:39.282Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential sums connected with Ramanujan's function τ(n)

Published online by Cambridge University Press:  26 February 2010

L. A. Parson  and
Mark Sheingorn
L. A. Parson
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, Ohio 43210, U.S.A.
Mark Sheingorn
Affiliation:
The Institute for Advanced Study, Princeton, New Jersey 08540, U.S.A.
Get access

Extract

This paper contains estimates of several exponential sums involving Fourier coefficients of certain modular forms. Although the questions which we consider date back, in some cases, to the twenties, our motivation is modern. All of these sums are connected with one approach to the problem of calculating the norm of the Poincaré 0-operator. In this section we state our results (and their antecedents) and then describe their relevance to the θ-operator problem. For simplicity we state and prove all our results for the modular cusp form of weight six, the famous discriminant function

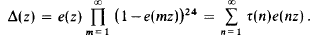
Type
Research Article
Information
Mathematika , Volume 29 , Issue 2 , December 1982 , pp. 270 - 277
Copyright
Copyright © University College London 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Deligne, P.. La conjecture de Weil. Inst. Hautes Études Sci. Publ. Math., 43 (1974), 273–307.Google Scholar
2.Kra, I.. Automorphic Forms and Kleinian Groups (Benjamin, Reading, MA, 1972).Google Scholar
3.Parson, L. A. and Sheingorn, M.. Bounding the norm of the Poincare λ-operator. Knopp, M. I., Ed., Analytic Number Theory, Lecture Notes in Mathematics, No. 899 (Springer-Verlag, New York, NY, 1981).Google Scholar
4.Rankin, R. A.. Ramanujan's function δ(n). Symposia on Theoretical Physics and Mathematics, Vol. 10 (Inst. Math. Sci., Madras), 1969 (Plenum, New York, 1970), 37–45.Google Scholar
5.Walfisz, A.. öber die Koeffizientensummen einiger Modulformen. Math. Ann., 108 (1933), 75–90.CrossRefGoogle Scholar
6.Wilton, J.. A note on Ramanujan's arithmetical function τ(n). Proc. Camb. Phil Soc, 25 (1929), 121–129.CrossRefGoogle Scholar