Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T17:59:59.211Z Has data issue: false hasContentIssue false
  • English
  • Français

The divisors of p-1

Published online by Cambridge University Press:  26 February 2010

R. R. Hall
R. R. Hall
Affiliation:
Department of Mathematics, University of York, Heslington, York.
Get access

Extract

Let τ(n; k, h) denote the number of divisors of n which are congruent to h (mod k), and τ(n; k) the number of divisors of n prime to k, so that

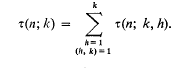
Let

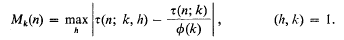
Erdős [1] proved that, if ε and η are fixed arbitrary positive numbers, then for almost all integers n ≤ x, we have

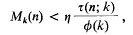
provided

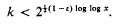
Hall and Sudbery [2] showed that it is sufficient that

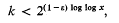
and apart from the ε, this upper bound for k is best possible, for it is clear that k must not exceed the normal order of τ(n). For n ≤ x, Hardy and Ramanujan [3] showed that this normal order is (log x)log 2 = 2 log log x.

Type
Research Article
Information
Mathematika , Volume 20 , Issue 1 , June 1973 , pp. 87 - 97
Copyright
Copyright © University College London 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Erdos, P., “On the distribution of divisors of integers in the residue classes (mod d)”, Bull. Math. Soc. Grece, 6 (1965), 27–36.Google Scholar
2. Hall, R. R. and Sudbery, A., “On a conjecture of Erdös and Rényi concerning Abelian groups”, J. London Math. Soc. (2), 6 (1972), 177–189.CrossRefGoogle Scholar
3. Hardy, G. H. and Ramanujan, S., “The normal number of prime factors of a number n”, Quarterly Journal, 48 (1917), 76–92.Google Scholar
4. Erdös, P., “On the normal number of prime factors of p – 1 and some related problems concerning Euler's ø-function”, Quarterly Journal, 6 (1935), 205–213.Google Scholar
5. Erdös, P. and Rényi, A., “Probabilistic methods in group theory”, Journal d'Analyse Math., 14 (1965), 127–138.CrossRefGoogle Scholar
6. Ramanujan, S., “Some formulae in the analytic theory of numbers”, Messenger of Mathematics, 45 (1915), 81–84.Google Scholar
7. Prachar, K., Primzahlverteilung (Springer, 1957).Google Scholar
8. Titchmarsh, E. C., The theory of the Riemann zeta-function (Oxford, 1951).Google Scholar