Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T17:19:11.138Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DIVISOR FUNCTION IN ARITHMETIC PROGRESSIONS MODULO PRIME POWERS

Part of: Finite fields and commutative rings (number-theoretic aspects) Multiplicative number theory

Published online by Cambridge University Press:  17 May 2016

Rizwanur Khan
Rizwanur Khan*
Affiliation:
Science Program, Texas A&M University at Qatar, Doha, Qatar email [email protected]
Get access

Abstract

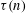We study the average value of the divisor function $\unicode[STIX]{x1D70F}(n)$ for 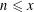$n\leqslant x$ with 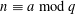$n\equiv a~\text{mod}~q$ . The divisor function is known to be evenly distributed over arithmetic progressions for all 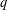$q$ that are a little smaller than 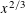$x^{2/3}$ . We show how to go past this barrier when 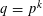$q=p^{k}$ for odd primes 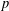$p$ and any fixed integer 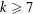$k\geqslant 7$ .

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11T23: Exponential sums
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 898 - 908
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Banks, W., Heath-Brown, R. and Shparlinski, I., On the average value of divisor sums in arithmetic progressions. Int. Math. Res. Not. IMRN 2005(1) 2005, 1–25, doi:10.1155/IMRN.2005.1.Google Scholar
Barban, M., Linnik, Yu. and Tshudakov, N., On prime numbers in an arithmetic progression with a prime-power difference. Acta Arith. 9 1964, 375–390.Google Scholar
Blomer, V., The average value of divisor sums in arithmetic progressions. Q. J. Math. 59(3) 2008, 275–286.Google Scholar
Blomer, V. and Milićević, D., p-adic analytic twists and strong subconvexity. Ann. Sci. Éc. Norm. Supér. (4) 48(3) 2015, 561–605.CrossRefGoogle Scholar
Blomer, V. and Milićević, D., The second moment of twisted modular L-functions. Geom. Funct. Anal. 25(2) 2015, 453–516.Google Scholar
Davenport, H., Multiplicative Number Theory (Graduate Texts in Mathematics 74 ), 3rd edn. Springer (New York, 2000), revised and with a preface by Hugh L. Montgomery.Google Scholar
Fouvry, É., Sur le problème des diviseurs de Titchmarsh. J. reine angew. Math. 357 1985, 51–76.Google Scholar
Fouvry, É. and Iwaniec, H., The divisor function over arithmetic progressions. Acta Arith. 61(3) 1992, 271–287, with an appendix by Nicholas Katz.Google Scholar
Fujii, A., Gallagher, P. and Montgomery, H., Some hybrid bounds for character sums and Dirichlet L-series. In Topics in Number Theory (Proceedings of the Colloquiums, Debrecen, 1974) (Colloquia Mathematica Societatis János Bolyai 13 ), North-Holland (Amsterdam, 1974), 41–57.Google Scholar
Gallagher, P., Primes in progressions to prime-power modulus. Invent. Math. 16 1972, 191–201.Google Scholar
Heath-Brown, R., Hybrid bounds for Dirichlet L-functions. Invent. Math. 47(2) 1978, 149–170.Google Scholar
Irving, A., The divisor function in arithmetic progressions to smooth moduli. Int. Math. Res. Not. IMRN 2015(15) 2015, 6675–6698, doi:10.1093/imrn/rnu149.CrossRefGoogle Scholar
Iwaniec, H., On zeros of Dirichlet’s L series. Invent. Math. 23 1974, 97–104.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (American Mathematical Society Colloquium Publications 53 ), American Mathematical Society (Providence, RI, 2004).Google Scholar
Koblitz, N., p-adic Numbers, p-adic Analysis, and Zeta-Functions (Graduate Texts in Mathematics 58 ), Springer (New York–Heidelberg, 1977).Google Scholar
Milićević, D., Sub-Weyl subconvexity for Dirichlet L-functions to powerful moduli. Compos. Math. 152(4) 2016, 825–875.Google Scholar
Munshi, R., Bounds for twisted symmetric square L-functions. J. reine angew. Math. 682 2013, 65–88.Google Scholar
Pongsriiam, P. and Vaughan, R. C., The divisor function on residue classes I. Acta Arith. 168(4) 2015, 369–382.CrossRefGoogle Scholar
Postnikov, A., On the sum of characters with respect to a modulus equal to a power of a prime number. Izv. Ross. Akad. Nauk SSSR Ser. Mat. 19 1955, 11–16.Google Scholar
Walfisz, A., Zur additiven Zahlentheorie. II. Math. Z. 40(1) 1936, 592–607.CrossRefGoogle Scholar
Young, M., The fourth moment of Dirichlet L-functions. Ann. of Math. (2) 173(1) 2011, 1–50.Google Scholar