Published online by Cambridge University Press: 26 February 2010
The reviewer [Math. Reviews, 32 (1966), 7526] has stated that he could not follow case (iii) of the proof of Lemma 7 and upon examination we find that the argument is incomplete (on p. 183, the degree of d1 may not be smaller than that of g). The following version of the proof (which is given with full details), circumvents the difficulty and has been designed to show, further, that the constant implied in the O-symbol is independent of the number of variables. This minor refinement may be of some interest as the corresponding estimates of Lang and Weil [Amer. J. Math., 76 (1954), 819–827; cf., Lemmas 1, 2 and Theorem 1] for general varieties over a finite field lack this feature. Throughout, we use the symbol deg F to denote the total degree of an element F of a polynomial domain 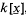 , where k = [p] is the field of residue classes mod p and
, where k = [p] is the field of residue classes mod p and 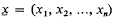 . Nr(†) will denote the number of r-tuples (xn−r+1, …, xn) ε kr with some specific property †. We prove that, if n ≥ 1 and f, g are elements of
. Nr(†) will denote the number of r-tuples (xn−r+1, …, xn) ε kr with some specific property †. We prove that, if n ≥ 1 and f, g are elements of 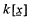 with no non-constant common factor in
with no non-constant common factor in 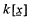 , i.e. (f, g)p = 1, then
, i.e. (f, g)p = 1, then
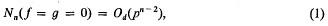
where the constant in the O-symbol depends only upon d = max (deg f, deg g). The argument is entirely elementary and uses a method of descent in which the number of variables n and the minimum degree, defined by
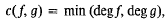
are simultaneously diminished at each step of the descent. It makes use of a corresponding (trivial) estimate for the case of one polynomial, i.e. if 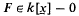 and ∂ = deg F, then Nn(F = 0) = O∂(pn−1). Thus, if f, g are disjoint in the sense that f ε k[x1, …, xr], g ε k[xr+1, …, xn] after a suitable permutation of x1, …, xn, then (f, g)p = 1 implies that
and ∂ = deg F, then Nn(F = 0) = O∂(pn−1). Thus, if f, g are disjoint in the sense that f ε k[x1, …, xr], g ε k[xr+1, …, xn] after a suitable permutation of x1, …, xn, then (f, g)p = 1 implies that
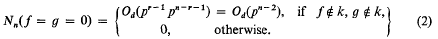
* Mathematika, 12 (1965), 176–192CrossRefGoogle Scholar.