Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dodson, M. M.
Rynne, B. P.
and
Vickers, J. A. G.
1990.
Diophantinc approximation by linear forms on manifolds.
Proceedings - Mathematical Sciences,
Vol. 100,
Issue. 3,
p.
221.
Rynne, Bryan P.
1992.
Regular and ubiquitous systems, and ‐dense sequences.
Mathematika,
Vol. 39,
Issue. 2,
p.
234.
Dickinson, H.
1993.
The Hausdorff dimension of systems of simultaneously small linear forms.
Mathematika,
Vol. 40,
Issue. 2,
p.
367.
Velani, S. L.
1993.
Diophantine approximation and Hausdorff dimension in Fuchsian groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 2,
p.
343.
Hill, Richard
and
Velani, Sanju L.
1995.
The ergodic theory of shrinking targets.
Inventiones Mathematicae,
Vol. 119,
Issue. 1,
p.
175.
Velani, Sanju L.
1996.
Geometrically finite groups, Khintchine-type theorems and Hausdorff dimension.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 120,
Issue. 4,
p.
647.
Dodson, M. M.
1997.
A note on metric inhomogeneous Diophantine approximation.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 62,
Issue. 2,
p.
175.
Dickinson, H.
1997.
A note on the theorem of Jarník-Besicovitch.
Glasgow Mathematical Journal,
Vol. 39,
Issue. 2,
p.
233.
Levesley, J.
1998.
A General Inhomogeneous Jarnik–Besicovitch Theorem.
Journal of Number Theory,
Vol. 71,
Issue. 1,
p.
65.
Rynne, Bryan P.
1998.
The Hausdorff Dimension of Sets Arising from Diophantine Approximation with a General Error Function.
Journal of Number Theory,
Vol. 71,
Issue. 2,
p.
166.
Dickinson, H.
and
Dodson, M. M.
2000.
Extremal manifolds and Hausdorff dimension.
Duke Mathematical Journal,
Vol. 101,
Issue. 2,
Kenneth, J. Falconer
2002.
Handbook of Measure Theory.
p.
1037.
Dodson, Maurice
2002.
Rigidity in Dynamics and Geometry.
p.
77.
Трубецкой, С
Troubetzkoy, S
Шмелинг, Й
and
Schmeling, J
2003.
Неоднородные диофантовы приближения и угловая возвращаемость для бильярдов в многоугольниках.
Математический сборник,
Vol. 194,
Issue. 2,
p.
129.
Bugeaud, Yann
2004.
Intersective sets and Diophantine approximation.
Michigan Mathematical Journal,
Vol. 52,
Issue. 3,
Druţu, Cornelia
2005.
Diophantine approximation on rational quadrics.
Mathematische Annalen,
Vol. 333,
Issue. 2,
p.
405.
Barral, Julien
and
Seuret, Stéphane
2005.
Combining Multifractal Additive and Multiplicative Chaos.
Communications in Mathematical Physics,
Vol. 257,
Issue. 2,
p.
473.
Durand, Arnaud
2008.
Ubiquitous systems and metric number theory.
Advances in Mathematics,
Vol. 218,
Issue. 2,
p.
368.
BARRAL, JULIEN
and
SEURET, STÉPHANE
2008.
Ubiquity and large intersections properties under digit frequencies constraints.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 145,
Issue. 3,
p.
527.
DURAND, ARNAUD
2008.
Sets with large intersection and ubiquity.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 1,
p.
119.
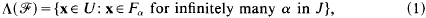
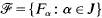 is a family of subsets of U indexed by a set J, are common in the theory of Diophantine approximation [4, 7, 18, 19]. They are also closely connected with exceptional sets arising in analysis and with sets of “small divisors” in dynamical systems [1, 8, 15”. When J is the set of positive integers ℕ, the set Λ(ℱ) is of course the lim-sup of the sequence of sets Fj, j = 1, 2,… [11, p. 1]. We will also call sets of the form (1), with the more general index set J, lim-sup sets. When such lim-sup sets have Lebesgue measure zero, it is of interest to determine their Hausdorff dimension. It is usually difficult to obtain a good lower bound for the Hausdorff dimension (and it can be much harder to determine than an upper bound). In this paper we will obtain a lower bound for the dimension of lim-sup sets of the form (1) for a fairly general class of families ℕ which includes a range of results in the theory of Diophantine approximation. This lower bound depends explicitly on the geometric structure and distribution in U of the sets Fα in ℕ.
is a family of subsets of U indexed by a set J, are common in the theory of Diophantine approximation [4, 7, 18, 19]. They are also closely connected with exceptional sets arising in analysis and with sets of “small divisors” in dynamical systems [1, 8, 15”. When J is the set of positive integers ℕ, the set Λ(ℱ) is of course the lim-sup of the sequence of sets Fj, j = 1, 2,… [11, p. 1]. We will also call sets of the form (1), with the more general index set J, lim-sup sets. When such lim-sup sets have Lebesgue measure zero, it is of interest to determine their Hausdorff dimension. It is usually difficult to obtain a good lower bound for the Hausdorff dimension (and it can be much harder to determine than an upper bound). In this paper we will obtain a lower bound for the dimension of lim-sup sets of the form (1) for a fairly general class of families ℕ which includes a range of results in the theory of Diophantine approximation. This lower bound depends explicitly on the geometric structure and distribution in U of the sets Fα in ℕ.