Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Faure, Henri
2007.
On the L2–discrepancies of van der Corput sequences.
PAMM,
Vol. 7,
Issue. 1,
p.
1022607.
Hofer, Roswitha
2018.
Halton-type sequences in rational bases in the ring of rational integers and in the ring of polynomials over a finite field.
Mathematics and Computers in Simulation,
Vol. 143,
Issue. ,
p.
78.


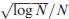 . This order is best possible by a result of K. Roth. The existence proof is constructive.
. This order is best possible by a result of K. Roth. The existence proof is constructive.