Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T02:41:01.957Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of sets of small or large boundary

Part of: Combinatorics

Published online by Cambridge University Press:  26 February 2010

Miklós Laczkovich
Miklós Laczkovich
Affiliation:
Department of Analysis, Eōtvōs Loránd University, Múzeum Krt, 6-8, Budapest, Hungary
Get access

Extract

We shall say that the sets A, B ⊂ Rk are equivalent, if they are equidecomposable using translations; that is, if there are finite decompositions 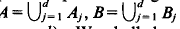and vectors x1,…, xd∈Rk such that Bj = Aj + xj, (j = 1,…,d). We shall denote this fact by 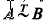In [3], Theorem 3 we proved that if A ⊂ Rk is a bounded measurable set of positive measure then A is equivalent to a cube provided that Δ(δA)<k where δA denotes the boundary of A and Δ(E) denotes the packing dimension (or box dimension or upper entropy index) of the bounded set E. This implies, in particular, that any bounded convex set of positive measure is equivalent to a cube. C. A. Rogers asked whether or not the set

MSC classification

Secondary: 05A18: Partitions of sets
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 290 - 304
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Edwards, R. E.. Fourier series (Holt, Rinehart and Winston, 1967).Google Scholar
2.Kuipers, L. and Niederreiter, H.. Uniform distribution of sequences (John Wiley & Sons, 1974).Google Scholar
3.Laczkovich, M.. Decomposition of sets with small boundary. J. London Math. Soc., 46 (1992), 58–64.CrossRefGoogle Scholar
4.Schmidt, W.. Metrical theorems on fractional parts of sequences. Trans. Amer. Math. Soc., 110 (1964), 493–518.Google Scholar
5.Tricot, C. Jr. Two definitions of fractional dimension. Math. Proc. Cambridge Phil. Soc., 91 (1982), 5774.Google Scholar
6.Wagon, S.. The Banach-Tarski paradox (Cambridge Univ. Press, 1986).Google Scholar