Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T19:14:07.003Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting points of bounded relative height

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  26 February 2010

Ana-Cecilia de la Maza
Ana-Cecilia de la Maza
Affiliation:
Instituto de Matemática y Física, Universidad de Talca, Casilla 747, Talca, Chile
Get access

Abstract

Let L/K be an extension of number fields and let 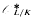be the subgroup of the unit group 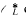consisting of the elements that are roots of units of 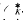. Denote by 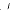(L/K, B) the number of points in 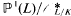with relative height in the sense of Bergé-Martinet at most B. Here ℙ1(L) stands for the one-dimensional projective space over L. In this paper is proved the formula 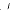(L/K, B) = CB2 + O(B2−1/[L:Q]), where C is a constant given in terms of invariants of L/K such as the regulators, class number and discriminant.

MSC classification

Secondary: 11R04: Algebraic numbers; rings of algebraic integers
Type
Research Article
Information
Mathematika , Volume 50 , Issue 1-2 , December 2003 , pp. 125 - 152
Copyright
Copyright © University College London 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[A]Apostol, T.. Introduction to Analytic Number Theory (Springer, 1976).Google Scholar
[BM1]Bcrge, A. M. and Martinet, J.. Notions relatives de regulateurs et de hauteurs. Ada Arith. 54 (1989), 156–170.Google Scholar
[BM2]Berge, A. M. and Martinet, J.. Minorations de hauteurs et petits regulateurs reiatifs. Sx00E9;m. Théorie des Nombres de Bordeaux, exposé 11 (1987– 1988).Google Scholar
[BC]Borevitch, Z. and Chafarevitch, I.. Théorie des Numbres (Paris: Gauthier-Villars, 1967).Google Scholar
[HW]Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers (Oxford: Oxford Science Publications, 1995).Google Scholar
[LI]Lang, S., Algebraic Number Theory (Reading. Mass: Addison-Wesley, 1970).Google Scholar
[L2]Lang, S.. Fundamentals of Diophtmtine Geometry (Berlin-Heidclbcrg-New York: Springer. 1983).Google Scholar
[S]Schanuel, S.. Heights in Number Fields. Hull. Soc. Math. France. 107 (1979). 433–449.CrossRefGoogle Scholar