Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T06:28:49.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Countable unions of compact spaces with the Namioka property

Part of: Basic constructions

Published online by Cambridge University Press:  26 February 2010

Richard Haydon
Richard Haydon
Affiliation:
Brasenose College, Oxford, OX1 4AJ
Get access

Extract

A compact space K is said to have the Namioka Property, or to belong to the class 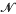*, if, for every Baire space B and every separately continuous function Ψ:B × K → ℝ, there is dense 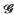δ subset H of B such that Ψ is (jointly) continuous at all points of H × K. Although the terminology is more recent, the idea of looking at properties of this kind goes back to Namioka's paper [6] on separate and joint continuity. Talagrand [8] gave the first example of a compact space that is not in 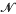* and it is now known [4] that there are even examples of scattered compact spaces that are not in 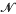*. On the other hand, many good classes of compact spaces have been shown to be contained in 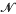*, probably the most general being the class of continuous images of Valdivia compacts [2]. The aim of this note is to prove the following stability result: a compact space which is a countable union of closed subsets with the Namioka Property does itself possess that property.

MSC classification

Secondary: 54B10: Product spaces
Type
Research Article
Information
Mathematika , Volume 41 , Issue 1 , June 1994 , pp. 141 - 144
Copyright
Copyright © University College London 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Debs, G.. Pointwise and uniform convergence on a Corson compact space. Topology and its Applications, 23 (1986), 299–303.CrossRefGoogle Scholar
2.Deville, R. and Godefroy, G.. Some applications of projectional resolutions of unity. Proc. London Math. Soc. (3), 67 (1993), 183–199.CrossRefGoogle Scholar
3.Deville, R., Godefroy, G. and Zizler, V.. Smoothness and renormings in Banach spaces. (Longman, Harlow, 1993).Google Scholar
4.Haydon, R. G.. A counterexample to several questions about scattered compact spaces. Bull. London Math. Soc, 22 (1990), 261–268.CrossRefGoogle Scholar
5.Jayne, J., Namioka, I. and Rogers, C. A.. Topological properties of Banach spaces. Proc. London Math. Soc, 66 (1993), 651– 672.CrossRefGoogle Scholar
6.Namioka, I.. Separate continuity and joint continuity. Pacific J. Math., 51 (1974), 515–531.CrossRefGoogle Scholar
7.Raymond, J. Saint. Jeux topologiques et espaces de Namioka. Proc. Amer. Math. Soc, 87 (1984), 499–504.CrossRefGoogle Scholar
8.Talagrand, M.. Espaces de Baire et espaces de Namioka. Math. Ann., 270 (1985), 159–164.CrossRefGoogle Scholar