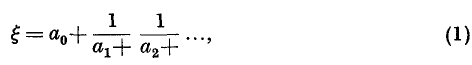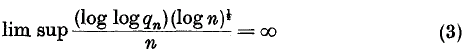Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Baker, A.
1964.
On Mahler's classification of transcendental numbers.
Acta Mathematica,
Vol. 111,
Issue. 0,
p.
97.
Burger, Edward B.
and
Struppeck, Thomas
1993.
On the frequency distribution of partial quotients ofU‐numbers.
Mathematika,
Vol. 40,
Issue. 2,
p.
215.
Queffélec, M.
1998.
Transcendance des fractions continues de Thue–Morse.
Journal of Number Theory,
Vol. 73,
Issue. 2,
p.
201.
Allouche, J.-P.
Davison, J.L.
Queffélec, M.
and
Zamboni, L.Q.
2001.
Transcendence of Sturmian or Morphic Continued Fractions.
Journal of Number Theory,
Vol. 91,
Issue. 1,
p.
39.
Mkaouar, Mohamed
2004.
Transcendance de certaines fractions continues dans le corps des séries formelles.
Journal of Algebra,
Vol. 281,
Issue. 2,
p.
502.
Hbaib, M.
Mkaouar, M.
and
Tounsi, K.
2006.
Un critére de transcendance de fractions continues dans Kp((X-1)).
Journal of Number Theory,
Vol. 116,
Issue. 1,
p.
140.
Adamczewski, Boris
and
Allouche, Jean-Paul
2007.
Reversals and palindromes in continued fractions.
Theoretical Computer Science,
Vol. 380,
Issue. 3,
p.
220.
Davison, J.L.
2007.
Quasi-periodic continued fractions.
Journal of Number Theory,
Vol. 127,
Issue. 2,
p.
272.
Adamczewski, Boris
and
Bugeaud, Yann
2007.
On the Maillet-Baker continued fractions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2007,
Issue. 606,
Chaichana, Tuangrat
and
Laohakosol, Vichian
2007.
Independence of continued fractions in the field of Laurent series.
Periodica Mathematica Hungarica,
Vol. 55,
Issue. 1,
p.
35.
CALTA, KARIANE
and
SCHMIDT, THOMAS A.
2012.
CONTINUED FRACTIONS FOR A CLASS OF TRIANGLE GROUPS.
Journal of the Australian Mathematical Society,
Vol. 93,
Issue. 1-2,
p.
21.
Bugeaud, Yann
2013.
Number Theory and Related Fields.
Vol. 43,
Issue. ,
p.
129.
Ammous, B.
Driss, S.
and
Hbaib, M.
2016.
Continued Fractions and Transcendence of Formal Power Series Over a Finite Field.
Mediterranean Journal of Mathematics,
Vol. 13,
Issue. 2,
p.
527.
Ooto, Tomohiro
2017.
Transcendental p-adic continued fractions.
Mathematische Zeitschrift,
Vol. 287,
Issue. 3-4,
p.
1053.
Masser, David
2021.
Alan Baker, FRS, 1939–2018.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 6,
p.
1916.
Ammous, B.
2023.
On the Maillet–Baker Ruban Continued Fractions in the $$p$$-Adic Field.
Mathematical Notes,
Vol. 114,
Issue. 5-6,
p.
659.
Masser FRS, David
2023.
Alan Baker. 19 August 1939—4 February 2018.
Biographical Memoirs of Fellows of the Royal Society,
Vol. 74,
Issue. ,
p.
9.
Ammous, B.
and
Ben Mahmoud, N.
2024.
On the quasi-periodic Schneider continued fractions.
Research in Number Theory,
Vol. 10,
Issue. 2,
Romeo, Giuliano
2024.
Continued fractions in the field of 𝑝-adic numbers.
Bulletin of the American Mathematical Society,
Vol. 61,
Issue. 2,
p.
343.
Longhi, Ignazio
Murru, Nadir
and
Saettone, Francesco M.
2025.
Heights and transcendence of p-adic continued fractions.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 204,
Issue. 1,
p.
129.