Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T22:34:49.584Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely right pure monoids: the general case

Part of: Semigroups

Published online by Cambridge University Press:  26 February 2010

Victoria A. R. Gould
Victoria A. R. Gould
Affiliation:
Dr. V. A. R. Gould, Department of Mathematics, University of York, Heslington, York, YO1 5DD.
Get access

Extract

A right S-system over a monoid S is a set A on which S acts unitarily on the right. That is, there is a function 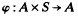A such that (φ,1)φ and (a, st)φ = ((a, s) t)φ for all a є A and for all s, t є S. We shall refer to right S-systems simply as S-systems. It is clear what is meant by S-homomorphism, S-subsystem etc.; further details of the terms used in this Introduction are given in Section 2.

MSC classification

Secondary: 20M99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 38 , Issue 1 , June 1991 , pp. 77 - 88
Copyright
Copyright © University College London 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

FG. Feller, E. H. and Gantos, R. L.. Completely right injective semigroups that are unions of groups. Glasgow Math. J., 12 (1971), 43–49.CrossRefGoogle Scholar
F. Fountain, J. B.. Completely right injective semigroups. Proc. London Math. Soc, 28 (1974), 28–44.CrossRefGoogle Scholar
Gl. Gould, V. A. R.. Completely right pure monoids. Proc. Royal Irish Acad., 87A (1987), 73–82.Google Scholar
G2. Gould, V. A. R.. Completely right pure monoids on which is a right congruence. Proc. Cambridge Phil. Soc, 107 (1990), 275–285.Google Scholar
Ha. Hall, T. E.. On regular semigroups whose idempotents form a subsemigroup. Bull. Australian Math. Soc, 1 (1969), 195–208.CrossRefGoogle Scholar
Ho. Howie, J. M.. An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
N. Normak, P.. Purity in the category of M-sets. Semigroup Forum, 20 (1982), 157–170.CrossRefGoogle Scholar