Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T19:00:36.623Z Has data issue: false hasContentIssue false
  • English
  • Français

A CODING OF BUNDLE GRAPHS AND THEIR EMBEDDINGS INTO BANACH SPACES

Part of: Graph theory Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  06 August 2018

Andrew Swift
Andrew Swift*
Affiliation:
Texas A&M University, College Station, TX 77843, U.S.A. email [email protected]
Get access

Abstract

The purpose of this article is to generalize some known characterizations of Banach space properties in terms of graph preclusion. In particular, it is shown that superreflexivity can be characterized by the non-equi-bi-Lipschitz embeddability of any family of bundle graphs generated by a non-trivial finitely branching bundle graph. It is likewise shown that asymptotic uniform convexifiability can be characterized within the class of reflexive Banach spaces with an unconditional asymptotic structure by the non-equi-bi-Lipschitz embeddability of any family of bundle graphs generated by a non-trivial 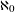$\aleph _{0}$-branching bundle graph. For the specific case of 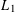$L_{1}$, it is shown that every countably branching bundle graph bi-Lipschitzly embeds into 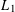$L_{1}$ with distortion no worse than 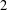$2$.

MSC classification

Primary: 46B85: Embeddings of discrete metric spaces into Banach spaces; applications in topology and computer science
Secondary: 46B06: Asymptotic theory of Banach spaces 46B07: Local theory of Banach spaces 05C78: Graph labelling (graceful graphs, bandwidth, etc.)
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 847 - 874
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Argyros, S., Motakis, P. and Sari, B., A study of conditional spreading sequences. J. Funct. Anal. 272(3) 2017, 1205–1257.Google Scholar
Ball, K., The Ribe programme. In Séminaire Bourbaki, Vol. 2011/2012, Exposés 1043–1058 (Astérisque 352 ), Société Mathématique de France (2013), Exp. No. 1047, viii, 147–159.Google Scholar
Baudier, F., Metrical characterization of super-reflexivity and linear type of Banach spaces. Arch. Math. 89 2007, 419–429.Google Scholar
Baudier, F., Causey, R., Dilworth, S., Kutzarova, D., Randrianarivony, N. L., Schlumprecht, Th. and Zhang, S., On the geometry of the countably branching diamond graphs. J. Funct. Anal. 273(10) 2017, 3150–3199.Google Scholar
Bourgain, J., The metrical interpretation of superreflexivity in Banach spaces. Israel J. Math. 56 1986, 222–230.Google Scholar
Brunel, A. and Sucheston, L., On J-convexity and some ergodic super-properties of Banach spaces. Trans. Amer. Math. Soc. 204 1975, 79–90.Google Scholar
Brunel, A. and Sucheston, L., Equal signs additive sequences in Banach spaces. J. Funct. Anal. 21(3) 1976, 286–304.Google Scholar
Chakrabarti, A., Jaffe, A., Lee, J. R. and Vincent, J., Embeddings of topological graphs: lossy invariants, linearization, and 2-sums. In Proceedings of the 2008 49th Annual IEEE Symposium on Foundations of Computer Science (October 25–28, 2008) , 761–770.Google Scholar
Dilworth, S. J., Kutzarova, D. and Randrianarivony, N. L., The transfer of property (𝛽) of Rolewicz by a uniform quotient map. Trans. Amer. Math. Soc. 368(9) 2016, 6253–6270.Google Scholar
Gupta, A., Newman, I., Rabinovich, Y. and Sinclair, A., Cuts, trees and ℓ 1 -embeddings of graphs. Combinatorica 24(2) 2004, 233–269.Google Scholar
Johnson, W. B. and Schechtman, G., Diamond graphs and super-reflexivity. J. Anal. 1(2) 2009, 177–189.Google Scholar
Laakso, T. J., Ahlfors Q-regular spaces with arbitrary Q > 1 admitting weak Poincaré inequality. Geom. Funct. Anal. 10 2000, 111–123.+1+admitting+weak+Poincaré+inequality.+Geom.+Funct.+Anal.+10+2000,+111–123.>Google Scholar
Lang, U. and Plaut, C., Bilipschitz embeddings of metric spaces into space forms. Geom. Dedicata 87(1–3) 2001, 285–307.Google Scholar
Lee, J. R. and Raghavendra, P., Coarse differentiation and multi-flows in planar graphs. Discrete Comput. Geom. 43(2) 2010, 346–362.Google Scholar
Naor, A., An introduction to the Ribe progam. Jpn. J. Math. 7(2) 2012, 167–233.Google Scholar
Newman, I. and Rabinovich, Y., A lower bound on the distortion of embedding planar metrics into Euclidean space. Discrete Comput. Geom. 29(1) 2003, 77–81.Google Scholar
Ostrovskii, M. I. and Randrianantoanina, B., A new approach to low-distortion embeddings of finite meric spaces into non-superreflexive Banach spaces. J. Funct. Anal. 273(2) 2017, 598–651.Google Scholar
Pisier, G., Martingales in Banach Spaces (Cambridge Studies in Advanced Mathematics 155 ), Cambridge University Press (Cambridge, 2016).Google Scholar