Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T17:38:57.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Character sums with exponential functions

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  26 February 2010

John B. Friedlander ,
Jan Hansen  and
Igor E. Shparlinski
John B. Friedlander
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 3G3, Canada. E-mail: [email protected]
Jan Hansen
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia. E-mail: [email protected]
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia. E-mail: [email protected]
Get access

Abstract

Let ϑ be an integer of multiplicative order t≥1 modulo a prime p. Sums of the form

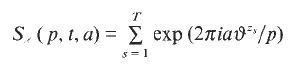
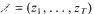are introduced and estimated, with a sequence such that kz1, …, kzT is a permutation of z1, …, zT, both sequences taken modulo t, for sufficiently many distinct modulo t values of k. Such sequences include

xn for x = 1 ,…,t with an integer n≥1;

xn for x = 1 ,…,t and gcd (x, t) = 1 with an integer n≥1;

ex for x = 1 ,…,T with an integer e, where T is the period of the sequence ex modulo t.

Some of the results can be extended to composite moduli and to sums of multiplicative characters as well. Character sums with the above sequences have some cryptographic motivation and applications and have been considered in several papers by J. B. Friedlander, D. Lieman and I. E. Shparlinski. In particular several previous bounds are generalized and improved.

MSC classification

Secondary: 11L07: Estimates on exponential sums
Type
Research Article
Information
Mathematika , Volume 47 , Issue 1-2 , December 2000 , pp. 75 - 85
Copyright
Copyright © University College London 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Canetti, R., Friedlander, J. B., Konyagin, S., Larsen, M., Lieman, D. and Shparlinski, I. E.. On the statistical properties of Diffie-Hellman distributions. Israel J. Math. 120 (2000), 23–46.CrossRefGoogle Scholar
2.Canetti, R., Friedlander, J. B. and Shparlinski, I. E.. On certain exponential sums and the distribution of Diffie-Hellman triples. J. London Math. Soc., 59 (1999), 799–812.CrossRefGoogle Scholar
3.Friedlander, J. B., Lieman, D. and Shparlinski, I. E.. On the distribution of the RSA generator. Proc. Intern. Conf. on Sequences and Their Applications (SETA '98), Singapore, Springer-Verlag (London, 1999), 205–212.CrossRefGoogle Scholar
4.Friedlander, J. B. and Shparlinski, I. E.. On the distribution of the power generator. Math. Comp. 70 (2001), 1575–1589.CrossRefGoogle Scholar
5.Konyagin, S. and Shparlinski, I. E.. Character Sums with Exponential Functions and their Applications, Cambridge Univ. Press (Cambridge, 1999).CrossRefGoogle Scholar
6.Korobov, N. M.. On the distribution of digits in periodic fractions. Math. USSR-Sbornik, 18 (1972), 659–676.CrossRefGoogle Scholar
7.Korobov, N. M.. Exponential Sums and their Applications. Kluwer Acad. Publ. (Dordrecht, 1992).CrossRefGoogle Scholar
8.Lidl, R. and Niederreiter, H.. Finite Fields, Cambridge University Press (Cambridge, 1997).Google Scholar
9.Lieman, D. and Shparlinski, I. E.. On a new exponential sum. Canad. Math. Bull. 44 (2001), 87–92.CrossRefGoogle Scholar
10.Niederreiter, H.. Quasi-Monte Carlo methods and pseudo-random numbers. Bull. Amer. Math. Soc., 84 (1978), 957–1041.CrossRefGoogle Scholar
11.Niederreiter, H.. Random Number Generation and Quasi-Monte Carlo Methods. SIAM Press (Philadelphia, 1992).CrossRefGoogle Scholar
12.Ribenboim, P.. The New Book of Prime Number Records, Springer-Verlag (New York, 1996).CrossRefGoogle Scholar
13.Vinogradov, I. M.. Elements of Number Theory, Dover Publ. (New York, 1954).Google Scholar