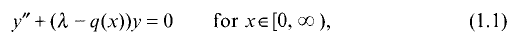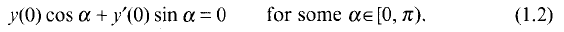Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Riehl, S. M.
2003.
The form of the spectral functions associated with Dirac equations.
Mathematika,
Vol. 50,
Issue. 1-2,
p.
153.
Gilbert, D.J.
Harris, B.J.
and
Riehl, S.M.
2004.
The spectral function for Sturm–Liouville problems where the potential is of Wigner–von Neumann type or slowly decaying.
Journal of Differential Equations,
Vol. 201,
Issue. 1,
p.
139.
Pechentsov, A. S.
and
Popov, A. Yu.
2007.
Asymptotic behavior of the spectral measure density of a singular Sturm-Liouville operator as λ → −∞.
Doklady Mathematics,
Vol. 75,
Issue. 3,
p.
374.
Gilbert, D. J.
Harris, B. J.
and
Riehl, S. M.
2009.
Methods of Spectral Analysis in Mathematical Physics.
Vol. 186,
Issue. ,
p.
217.
Brändas, Erkki J.
2010.
Partitioning technique for open systems.
Molecular Physics,
Vol. 108,
Issue. 21-23,
p.
3259.
Brändas, Erkki J.
2012.
Vol. 63,
Issue. ,
p.
33.