Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T19:38:41.023Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded representations of integers by quadratic forms

Published online by Cambridge University Press:  26 February 2010

G. L. Watson
G. L. Watson
Affiliation:
University College, London.
Get access

Extract

Let ƒ = ƒ(x1, …, xk) be a quadratic form in k variables, which has integral coefficients and is not degenerate. Let n ≠ 0 be any integer representable by ƒ, that is, such that the equation

is soluble in integers x1, …, xk. We shall call a solution of (1) a bounded representation of n by ƒ if it satisfies

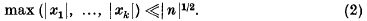
Type
Research Article
Information
Mathematika , Volume 4 , Issue 1 , June 1957 , pp. 17 - 24
Copyright
Copyright © University College London 1957

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 17 note * See, e.g., Landau, , Vorlesungen über Zahlentheorie I, 141, Satz 203.Google Scholar

page 17 note † Meyer, A., Vierteljahrsschrift der Naturforschenden Ges. in Zürich, 29 (1884), 209–222.Google Scholar

page 19 note * The determinant of g itself may be fractional, if g has product terms with odd coefficients.

page 19 note † For a simple proof, see Pall, Gordon, "On the order invariants of integral quadratic forms", Quart. J. of Math. (Oxford), 6 (1935), 30–51 (35, Lemma 2).CrossRefGoogle Scholar

page 20 note * An appeal to this theory can be avoided by remarking that Lemma 1 (ii) continues t o hold if q is any square-free positive integer which is relatively prime to the fixed number 2|Δ|. The existence of such an integer satisfying (16) and (17), and also relatively prime to d (as we require later) is easily proved.

page 22 note * See, for example, Hermite, Oeuvres I, 122–135.