Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rush, J. A.
1994.
An indexed set of density bounds on lattice packings.
Geometriae Dedicata,
Vol. 53,
Issue. 2,
p.
217.
Rush, J. A.
1995.
Compositions of sums of absolute powers.
Geometriae Dedicata,
Vol. 57,
Issue. 2,
p.
135.
Rush, J. A.
1996.
Lattice packing of nearly-euclidean balls in spaces of even dimension.
Proceedings of the Edinburgh Mathematical Society,
Vol. 39,
Issue. 1,
p.
163.
Tóth, G. Fejes
Fodor, F.
and
Vígh, V.
2015.
The Packing Density of the $$n$$ n -Dimensional Cross-Polytope.
Discrete & Computational Geometry,
Vol. 54,
Issue. 1,
p.
182.
Kovačević, Mladen
2022.
Lattice packings of cross‐polytopes from Reed–Solomon codes and Sidon sets.
Bulletin of the London Mathematical Society,
Vol. 54,
Issue. 6,
p.
2372.


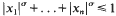 is 2
is 2