Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stephens, P. J.
1969.
An average result for Artin's conjecture.
Mathematika,
Vol. 16,
Issue. 2,
p.
178.
Goldfeld, Morris
1973.
A large sieve for a class of non-abelianL-functions.
Israel Journal of Mathematics,
Vol. 14,
Issue. 1,
p.
39.
Antoniadis, Jannis A.
1984.
�ber die Periodenl�nge modp einer Klasse rekursiver Folgen.
Archiv der Mathematik,
Vol. 42,
Issue. 3,
p.
242.
Hinz, J�rgen G.
1984.
Some applications of Sieve methods in algebraic number fields.
Manuscripta Mathematica,
Vol. 48,
Issue. 1-3,
p.
117.
Hinz, Jürgen G
1986.
A note on Artin's conjecture in algebraic number fields.
Journal of Number Theory,
Vol. 22,
Issue. 3,
p.
334.
Li, Shuguang
1999.
On extending Artin's conjecture to composite moduli.
Mathematika,
Vol. 46,
Issue. 2,
p.
373.
Moree, Pieter
1999.
On Primes in Arithmetic Progression Having a Prescribed Primitive Root.
Journal of Number Theory,
Vol. 78,
Issue. 1,
p.
85.
Li, Shuguang
2000.
Artin's Conjecture on Average for Composite Moduli.
Journal of Number Theory,
Vol. 84,
Issue. 1,
p.
93.
Moree, Pieter
2000.
Asymptotically Exact Heuristics for (Near) Primitive Roots.
Journal of Number Theory,
Vol. 83,
Issue. 1,
p.
155.


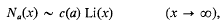
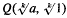 .
.