Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T22:29:54.191Z Has data issue: false hasContentIssue false
  • English
  • Français

ARITHMETIC PROGRESSIONS IN SETS OF SMALL DOUBLING

Part of: Sequences and sets

Published online by Cambridge University Press:  17 February 2016

Kevin Henriot
Kevin Henriot*
Affiliation:
Department of Mathematics, University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver BC V6T 1Z2, Canada email [email protected]
Get access

Abstract

We show that if a finite, large enough subset 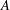$A$ of an arbitrary abelian group 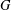$G$ satisfies the small doubling condition 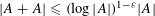$|A+A|\leqslant (\log |A|)^{1-{\it\varepsilon}}|A|$, then 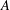$A$ must contain a three-term arithmetic progression whose terms are not all equal, and 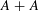$A+A$ must contain an arithmetic progression or a coset of a subgroup, either of which is of size at least 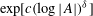$\exp [c(\log |A|)^{{\it\delta}}]$. This extends analogous results obtained by Sanders, and by Croot, Łaba and Sisask in the case where 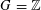$G=\mathbb{Z}$.

MSC classification

Primary: 11B13: Additive bases, including sumsets 11B30: Arithmetic combinatorics; higher degree uniformity
Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 587 - 613
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bateman, M. and Katz, N. H., New bounds on cap sets. J. Amer. Math. Soc. 25(2) 2012, 585–613.Google Scholar
Bourgain, J., On arithmetic progressions in sums of sets of integers. In A Tribute to Paul Erdős, Cambridge University Press (Cambridge, 1990), 105–109.CrossRefGoogle Scholar
Bourgain, J., On triples in arithmetic progression. Geom. Funct. Anal. 9(5) 1999, 968–984.Google Scholar
Croot, E., Łaba, I. and Sisask, O., Arithmetic progressions in sumsets and L p -almost-periodicity. Combin. Probab. Comput. 22(3) 2013, 351–365.Google Scholar
Croot, E. and Sisask, O., A probabilistic technique for finding almost-periods of convolutions. Geom. Funct. Anal. 20(6) 2010, 1367–1396.Google Scholar
Green, B., Arithmetic progressions in sumsets. Geom. Funct. Anal. 12(3) 2002, 584–597.Google Scholar
Green, B. and Ruzsa, I. Z., Freiman’s theorem in an arbitrary abelian group. J. Lond. Math. Soc. (2) 75(1) 2007, 163–175.Google Scholar
Green, B. and Sanders, T., A quantitative version of the idempotent theorem in harmonic analysis. Ann. of Math. (2) 168(3) 2008, 1025–1054.Google Scholar
Hatami, H., Fourier analysis of finite abelian groups. In Lecture Notes, 2011, http://cs.mcgill.ca/∼hatami/comp760-2011/.Google Scholar
Hegyvári, N., Hennecart, F. and Plagne, A., A proof of two Erdős’ conjectures on restricted addition and further results. J. Reine Angew. Math. 560 2003, 199–220.Google Scholar
Henriot, K., Bourgain’s bounds for Roth’s theorem. In Expository Note, 2013, http://www.math.ubc.ca/∼khenriot/notes/bourgainroth.pdf.Google Scholar
Henriot, K., Notes on the Croot–Sisask lemma. In Expository Note, 2013, http://www.math.ubc.ca/∼khenriot/notes/almostp.pdf.Google Scholar
Lev, V. F., Progression-free sets in finite abelian groups. J. Number Theory 104(1) 2004, 162–169.Google Scholar
Lyall, N., Behrend’s example. In Expository Note, 2005.Google Scholar
Petridis, G., New proofs of Plünnecke-type estimates for product sets in groups. Combinatorica 32(6) 2012, 721–733.Google Scholar
Roth, K. F., On certain sets of integers. J. Lond. Math. Soc. 28(1) 1953, 104–109.Google Scholar
Ruzsa, I. Z., Arithmetical progressions and the number of sums. Period. Math. Hungar. 25(1) 1992, 105–111.Google Scholar
Sanders, T., Roth’s theorem in ℤ4 n . Anal. PDE 2(2) 2009, 211–234.Google Scholar
Sanders, T., Three-term arithmetic progressions and sumsets. Proc. Edinb. Math. Soc. (2) 52(1) 2009, 211–233.Google Scholar
Sanders, T., Green’s sumset problem at density one half. Acta Arith. 146(1) 2011, 91–101.Google Scholar
Sanders, T., On Roth’s theorem on progressions. Ann. of Math. (2) 174(1) 2011, 619–636.Google Scholar
Sanders, T., On certain other sets of integers. J. Anal. Math. 116(1) 2012, 53–82.Google Scholar
Sanders, T., On the Bogolyubov–Ruzsa lemma. Anal. PDE 5(3) 2012, 627–655.Google Scholar
Sanders, T., The structure theory of set addition revisited. Bull. Amer. Math. Soc. (N.S.) 50(1) 2013, 93–127.Google Scholar
Schoen, T., The cardinality of restricted sumsets. J. Number Theory 96(1) 2002, 48–54.Google Scholar
Solymosi, J., Arithmetic progressions in sets with small sumsets. Combin. Probab. Comput. 15(4) 2006, 597–603.CrossRefGoogle Scholar
Stanchescu, Y. V., Planar sets containing no three collinear points and non-averaging sets of integers. Discrete Math. 256(1–2) 2002, 387–395.Google Scholar
Tao, T. and Vu, V. H., Additive Combinatorics (Cambridge Studies in Advanced Mathematics 105 ), Cambridge University Press (Cambridge, 2010).Google Scholar