Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T16:50:09.021Z Has data issue: false hasContentIssue false
  • English
  • Français

An integral mean inequality for starlike functions

Part of: Geometric function theory

Published online by Cambridge University Press:  26 February 2010

J. B. Twomey
J. B. Twomey
Affiliation:
Department of Mathematics, University College, Cork, Ireland.
Get access

Extract

A function

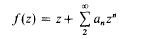
analytic and univalent in U = {z: |z| < 1} is said to be starlike there, if f(U) is f starshaped with respect to the origin, that is, if w ε f(U) implies tw ε f(U) for 0 ≤t ≤ 1. We denote by S* the class of all such functions. The Koebe function; k(z) = z(l – z)-2, z ε U, maps U onto the complex plane minus a slit along the I negative real axis from - ¼ to ∞, and thus belongs to the class S*. Recently Leung [4] has shown that, if

then, for f ε S*,

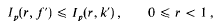
for every p > 0.

MSC classification

Secondary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Type
Research Article
Information
Mathematika , Volume 28 , Issue 1 , June 1981 , pp. 88 - 98
Copyright
Copyright © University College London 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Hayman, W. K.. “On functions with positive real part“, J. London Math. Soc, 36 (1961), 35–48.Google Scholar
2.Holland, F. and Thomas, D. K.. “The area theorem for starlike functions”, J. London Math. Soc. (2), 1 (1969), 127–134.CrossRefGoogle Scholar
3.Keogh, F. R.. “Some theorems on conformal mapping of bounded star-shaped domains”, Proc. London Math. Soc. (3), 9 (1959), 481–491.CrossRefGoogle Scholar
4.Leung, Y. J.. “Integral means of the derivatives of some univalent functions”, Bull. London Math. Soc, (1979), 289–294.Google Scholar
5.Pommerenke, C.. “On starlike and convex functions”, J. London Math. Soc, 37 (1962), 209–224.Google Scholar
6.Pommerenke, C.. Univalent functions (Vandenhoeck and Ruprecht, 1975).Google Scholar
7.Royden, H. L.. Real Analysis, Second Edition (Macmillan, 1968).Google Scholar
8.Seidel, W. and Walsh, J. L.. “On the derivatives of functions analytic in the unit circle and their radii of univalence and of p-value”, Trans. Amer. Math. Soc, 52 (1942), 128–216.Google Scholar
9.Thomas, D. K.. “A note on starlike functions”, J. London Math. Soc, 43 (1968), 703–706.CrossRefGoogle Scholar
10.Twomey, J. B.. “On the derivative of a starlike function”, J. London Math. Soc. (2), 2 (1970), 99–110.CrossRefGoogle Scholar
11.Twomey, J. B.. “On starlike functions”, Proc. American Math. Soc, 24 (1970), 95–97.Google Scholar
12.Twomey, J. B.. “On bounded starlike functions”, Jour. D'Analyse Math., 24 (1971), 191–204.Google Scholar