It was proved by Heilbronn that if ε > 0, N > 1 and ϑ is any real number then there exists an integer n satisfying 1 ≤ n ≤ N such that

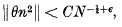
where C depends only on ε. Here ║α║ denotes the difference between α and the nearest integer, taken positively. Professor Heilbronn has remarked (in conversation) that the exponent of N cannot be decreased beyond -1, since if p is an odd prime and a is not divisible by p then

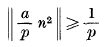
for 1 ≤ n ≤ p—1. He has also remarked that if one could improve the exponent of N to -1 + η, say, it would follow that the absolutely least quadratic non-residue (mod p) is less than Cpn. For if a is a quadratic non-residue (mod p) then so is each of the numbers an2 (1 ≤ n ≤ p—1) and ║an2/p║<Cp-1+η implies that an2 is congruent (mod p) to a number of absolute value less than Cpη.