Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T21:00:10.811Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EXPLICIT DIAGONAL RESOLUTION FOR A NON-ABELIAN METACYCLIC GROUP

Part of: Homological methods Representation theory of groups

Published online by Cambridge University Press:  23 March 2017

J. J. Remez
J. J. Remez*
Affiliation:
Department of Mathematics, University College London, Gower Street, London, WC1E 6BT, U.K. email [email protected]
Get access

Abstract

We consider the notion of a free resolution. In general, a free resolution can be of any length depending on the group ring under investigation. The metacyclic groups 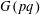$G(pq)$ however admit periodic resolutions. In the particular case of 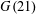$G(21)$ it is possible to achieve a fully diagonalized resolution. In order to achieve a diagonal resolution, we obtain a complete list of indecomposable modules over 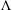$\unicode[STIX]{x1D6EC}$. Such a list aids the decomposition of the augmentation ideal (the first syzygy) into a direct sum of indecomposable modules. Therefore, we are able to achieve a diagonalized map here. From this point it is possible to decompose all of the remaining syzygies in terms of indecomposable modules, leaving a diagonal resolution.

MSC classification

Primary: 16E05: Syzygies, resolutions, complexes 20C10: Integral representations of finite groups
Type
Research Article
Information
Mathematika , Volume 63 , Issue 2 , 2017 , pp. 499 - 517
Copyright
Copyright © University College London 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cartan, H. and Eilenberg, S., Homological Algebra, Princeton University Press (1956).Google Scholar
Curtis, C. W. and Reiner, I., Methods of Representation Theory, Vol. I, Wiley-Interscience (1981).Google Scholar
Curtis, C. W. and Reiner, I., Methods of Representation Theory, Vol. II, Wiley-Interscience (1987).Google Scholar
Fox, R. H., Free differential calculus V. Ann. of Math. (2) 71 1960, 408–422.CrossRefGoogle Scholar
Galovich, S., Reiner, I. and Ullom, S., Class groups for integral representations of metacyclic groups. Mathematika 19 1972, 105–111.CrossRefGoogle Scholar
Hilbert, D., Theory of Algebraic Invariants (Cambridge Mathematical Library), Cambridge University Press (1993).Google Scholar
Johnson, F. E. A., Stable Modules and the D(2)-Problem (LMS Lecture Notes in Mathematics 301 ), Cambridge University Press (2003).Google Scholar
Johnson, F. E. A., Syzygies and Homotopy Theory, Springer (2012).Google Scholar
Milnor, J., Introduction to Algebraic K-Theory (Annals of Mathematics Studies), Princeton University Press (1971).Google Scholar
Pu, L. C., Integral representations of non-abelian groups of order pq . Michigan Math. J. 12 1965, 231–246.CrossRefGoogle Scholar
Rosen, M., Representations of twisted group rings. PhD Thesis, Princeton University, 1963.Google Scholar
Swan, R. G., Periodic resolutions for finite groups. Ann. of Math. (2) 72 1960, 267–291.CrossRefGoogle Scholar
Wall, C. T. C., Finiteness conditions for CW-complexes. Ann. of Math. (2) 81 1965, 56–69.Google Scholar
Wolf, J., Spaces of Constant Curvature, McGraw-Hill (1967).Google Scholar