Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:29:39.447Z Has data issue: false hasContentIssue false
  • English
  • Français

An example concerning completion regular measures, images of measurable sets and measurable selections

Part of: Classical measure theory

Published online by Cambridge University Press:  26 February 2010

A. G. A. G. Babiker  and
J. D. Knowles
A. G. A. G. Babiker
Affiliation:
Westfield College, London.
J. D. Knowles
Affiliation:
Westfield College, London.
Get access

Extract

We exhibit (§2) an example of §a compact Hausdorff space 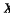supporting a Radon probability measure μ and a continuous map ø : X → I, when I is the closed unit interval, for which the image measure ø(μ) is Lebesgue measur m with the properties:

(i) there exists an open set G ⊂ X for which ø(G) is not m-measurable;

(ii) μ is a non-atomic non-completion regular measure;

(iii) the measure algebras (X, μ) and (I, m) are isomorphic but for no choice c sets B ⊂ X, B′ ⊂ I of measure zero are 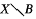and 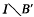homeomorphic

(iv) there exists a selection p : I → X (i.e. p(t) ∊ ø−1(t) for all t ∊ I) which i Borel m-measurable, but there is no Lusin m-measurable selection.

MSC classification

Secondary: 28A05: Classes of sets (Borel fields, $sigma$-rings, etc.), measurable sets, Suslin sets, analytic sets
Type
Research Article
Information
Mathematika , Volume 25 , Issue 1 , June 1978 , pp. 120 - 124
Copyright
Copyright © University College London 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Boge, W., Krickeberg, K. and Papangelou, F.. “Uber die dem Lebesgueschen Mass Isomorphen topologischen Massraume”, Manuscripta Math, 1 (1969), 59–77.Google Scholar
2.Edgar, G. A.. “Measurable weak sections”, Illinois J. Math., 20 (1976), 630–646.CrossRefGoogle Scholar
3.Gelbaum, B. B.. “Cantor sets in metric measure spaces”, Proc. Amer. Math. Soc, 24 (1970) 341–343.Google Scholar
4.Gillman, L. and Jerison, M.. Rings of continuous functions (Van Nostrand, 1960).CrossRefGoogle Scholar
5.A., and Ionescu Tulcea, C.. Topics in the theory of lifting (Springer-Verlag, 1969).Google Scholar
6.Knowles, J. D.. “Measures on topological spaces”, Proc. London Math. Soc, 17 (1967), 139–150.CrossRefGoogle Scholar
7.Knowles, J. D. and Rogers, C. A.. “Descriptive Baire sets”, Proc. Roy. Soc, A, 291 (1966; 353–367.Google Scholar
8.Maharam, D.. “On homogeneous measure algebras”, Proc. Nat. Acad. Sci., 28 (1942), 108–111CrossRefGoogle ScholarPubMed
9.Oxtoby, J. C.. “Homeomorphic measures in metric spaces”, Proc. Amer. Math. Soc, 24 (1970 419–23.CrossRefGoogle Scholar
10.Rogers, C. A.. “Analytic sets in Hausdorff spaces”, Mathematika, 11 (1964), 1–8.Google Scholar
11.Schwartz, L.. Radon measures on arbitrary topological spaces and cylindrical measures (Oxford 1973).Google Scholar
12.Sion, M.. “Topological and measure theoretic properties of analytic sets”, Proc. Amer. Mat Soc, 11 (1960), 769–776.Google Scholar