Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T17:52:42.675Z Has data issue: false hasContentIssue false
  • English
  • Français

The amount of overlapping in partial coverings of space by equal spheres

Published online by Cambridge University Press:  26 February 2010

P. Erdős ,
L. Few  and
C. A. Rogers
P. Erdős
Affiliation:
University College, and London.
L. Few
Affiliation:
University College, and London.
C. A. Rogers
Affiliation:
University College, and London.
Get access

Extract

We say that a system ∑ of equal spheres S1S2, … covers a proportion θ of n-dimensional space, if the limit, as the side of the cube C tends to infinity, of the ratio

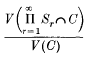
of the volume of C covered by the spheres to the volume of C, exists and has the value θ. We say that such a system ∑ has density δ, if the corresponding ratio

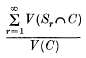
has the limit δ as the side of the cube C tends to infinity. We confine our attention to systems ∑ for which both limits exist. It is clear that δ = θ, if no two spheres of the system overlap, i.e. if we have a. packing; and that, in general, the difference δ-θ is a measure of the amount of overlapping.

Type
Research Article
Information
Mathematika , Volume 11 , Issue 2 , December 1964 , pp. 171 - 184
Copyright
Copyright © University College London 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Minkowski, H., “Diskontinuitätsbereich für arithmetische Aequivalenz”, J. reine angew. Math., 129 (1905), 220–274.Google Scholar
2. Blichfeldt, H. F., “The minimum value of quadratic forms, and the closest packing of spheres”, Math. Annalen, 101 (1929), 605–608.CrossRefGoogle Scholar
3. Davenport, H. and Rogers, C. A., “Hlawka's theorem in the geometry of numbers”, Duke Math. J., 14 (1947), 367–375.CrossRefGoogle Scholar
4. Schmidt, W., “On the Minkowski-Hlawka Theorem”, Illinois J. of Math., 7 (1963). 18–23 and 714.Google Scholar
5. Rogers, C. A., “The packing of equal spheres”, Proc. London Math. Soc. (3), 8 (1958), 609–620.CrossRefGoogle Scholar
6. Bambah, R. P. and Davenport, H., “The covering of n-dimensional space by spheres”, Journal London Math. Soc., 27 (1952), 224–229.Google Scholar
7. Erdős, P. and Rogers, C. A., “The covering of n-dimensional space by spheres”, Journal London Math. Soc., 28 (1953), 287–293.Google Scholar
8. Coxeter, H. S. M., Few, L. and Rogers, C. A., “Covering space with equal spheres”, Mathematika, 6 (1959), 147–157.Google Scholar
9. Rogers, C. A., “Lattice coverings of space with convex bodies”, Journal London Math. Soc., 33 (1958), 208–212.Google Scholar
10. Rogers, C. A., “Lattice coverings of space: the Minkowski-Hlawka theorem”, Proc London Math. Soc. (3), 8 (1958), 447–465.CrossRefGoogle Scholar
11. Rogers, C. A., “A note on coverings”, Mathematika, 4 (1957), 1–6.CrossRefGoogle Scholar
12. Rogers, C. A., Packing and covering (Cambridge, 1964).Google Scholar