No CrossRef data available.
Published online by Cambridge University Press: 21 December 2009
Let 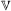 be a finite-dimensional vector space over a square-root closed ordered field
be a finite-dimensional vector space over a square-root closed ordered field 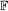 (this restriction permits an inner product with corresponding norm to be imposed on
(this restriction permits an inner product with corresponding norm to be imposed on 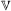 ). Many properties of the family
). Many properties of the family 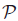 :=
:=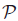 (
(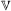 ) of convex polytopes in
) of convex polytopes in 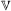 can be expressed in terms of valuations (or finitely additive measures). Valuations such as volume, surface area and the Euler characteristic are translation invariant, but others, such as the moment vector and inertia tensor, display a polynomial behaviour under translation. The common framework for such valuations is the polytope (or Minkowski) ring Π:=Π(
can be expressed in terms of valuations (or finitely additive measures). Valuations such as volume, surface area and the Euler characteristic are translation invariant, but others, such as the moment vector and inertia tensor, display a polynomial behaviour under translation. The common framework for such valuations is the polytope (or Minkowski) ring Π:=Π(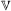 ), and its quotients under various powers of the ideal T of Π which is naturally associated with translations. A central result in the theory is that, in all but one trivial respect, the ring Π/T is actually a graded algebra over
), and its quotients under various powers of the ideal T of Π which is naturally associated with translations. A central result in the theory is that, in all but one trivial respect, the ring Π/T is actually a graded algebra over 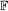 . Unfortunately, while the quotients Π/Tk+1 are still graded rings for k > 1, they now only possess a rational algebra structure; to obtain an algebra over
. Unfortunately, while the quotients Π/Tk+1 are still graded rings for k > 1, they now only possess a rational algebra structure; to obtain an algebra over 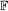 , some (weak) continuity assumptions have to be made, although these can be achieved algebraically, by factoring out a further ideal A, the algebra ideal.
, some (weak) continuity assumptions have to be made, although these can be achieved algebraically, by factoring out a further ideal A, the algebra ideal.