Published online by Cambridge University Press: 25 April 2018
We study a combinatorial problem that recently arose in the context of shape optimization: among all triangles with vertices 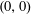 $(0,0)$,
$(0,0)$, 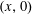 $(x,0)$, and
$(x,0)$, and 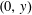 $(0,y)$ and fixed area, which one encloses the most lattice points from
$(0,y)$ and fixed area, which one encloses the most lattice points from 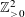 $\mathbb{Z}_{{>}0}^{2}$? Moreover, does its shape necessarily converge to the isosceles triangle
$\mathbb{Z}_{{>}0}^{2}$? Moreover, does its shape necessarily converge to the isosceles triangle 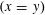 $(x=y)$ as the area becomes large? Laugesen and Liu suggested that, in contrast to similar problems, there might not be a limiting shape. We prove that the limiting set is indeed non-trivial and contains infinitely many elements. We also show that there exist “bad” areas where no triangle is particularly good at capturing lattice points and show that there exists an infinite set of slopes
$(x=y)$ as the area becomes large? Laugesen and Liu suggested that, in contrast to similar problems, there might not be a limiting shape. We prove that the limiting set is indeed non-trivial and contains infinitely many elements. We also show that there exist “bad” areas where no triangle is particularly good at capturing lattice points and show that there exists an infinite set of slopes 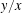 $y/x$ such that any associated triangle captures more lattice points than any other fixed triangle for infinitely many (and arbitrarily large) areas; this set of slopes is a fractal subset of
$y/x$ such that any associated triangle captures more lattice points than any other fixed triangle for infinitely many (and arbitrarily large) areas; this set of slopes is a fractal subset of 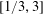 $[1/3,3]$ and has Minkowski dimension of at most
$[1/3,3]$ and has Minkowski dimension of at most 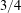 $3/4$.
$3/4$.