Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-11T11:45:24.286Z Has data issue: false hasContentIssue false
  • English
  • Français

Total scalar curvature and rigidity of minimal hypersurfaces in Euclidean space

Part of: Global differential geometry

Published online by Cambridge University Press:  26 February 2010

Gabjin Yun
Gabjin Yun
Affiliation:
Department of Mathematics, College of Science, Myong-Ji University, 38-2 San, Nam-Dong, Yongin, Kyunggi-do, 449-728, Korea.
Get access

Abstract

Let Mn, n ≥ 3, be a complete oriented minimal hypersurface in Euclidean space Rn+1. It is shown that, if the total scalar curvature on M is less than the n/2 power of 1/2Cs, where Cs is the Sobolev constant for M, and the square norm of the second fundamental form 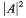is a L2 function, then M is a hyperplane.

MSC classification

Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Mathematika , Volume 48 , Issue 1-2 , December 2001 , pp. 247 - 251
Copyright
Copyright © University College London 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anderson, M. T.. The compactification of a minimal submanifold in Euclidean space by the Gauss map. Preprint.Google Scholar
2.Bérard, P., Remarques sur l'équation de J. Simons. Differential Geometry, Pitman Monographs Survey Pure Appl. Math. 52 (1991), 47–57.Google Scholar
3.Cao, H.-D.Shen, Y. and Zhu, S.. The structure of stable minimal hypersurfaces in Rn+1. Math. Res. Lett. 4 (1997), 637–644.CrossRefGoogle Scholar
4.DoCarmo, M. and Peng, C. K.. Stable minimal surfaces in R3 are planes. Bull. A.M.S. 1 (1979), 903–905.CrossRefGoogle Scholar
5.DoCarmo, M. and Peng, C. K.. Stable complete minimal hypersurfaces. Proc. Beijing Sympos. Differential Equations Differential Geom. 3 (1980), 1349–1358.Google Scholar
6.Fischer-Colbrie, D. and Schoen, R.. The structure of complete stable minimal surfaces in 3-manifolds of nonnegative scalar curvature. Comm. Pure Appl. Math. 33 (1980), 199–211.CrossRefGoogle Scholar
7.Hoffman, D. and Spruck, J.. Sobolev and isoperimetric inequalities for Riemannian submanifolds. Comm. Pure Appl. Math. 27 (1974), 715–727.CrossRefGoogle Scholar
8.Kasue, A.. Gap theorems for minimal submanifolds of Euclidean space. J. Math. Soc. Japan 38 (1986), 473–492.CrossRefGoogle Scholar
9.Michael, J. and Simon, L.. Sobolev and mean-value inequalities on generalized submanifolds of Rn. Comm. Pure Appl. Math. 26 (1973), 361–379.CrossRefGoogle Scholar
10.Shen, Y.-B. and Zhu, X.-H.. On stable minimal hypersurfaces in Rn+1. Amer. J. Math. 120 (1998), 103–116.CrossRefGoogle Scholar
11.Shoen, R.Simon, L. and Yau, S.-Y.. Curvature estimates for minimal hypersurfaces. Acta Math. 134(1975), 275–288.CrossRefGoogle Scholar
12.Tysk, J.. Finiteness of index and total scalar curvature for minimal hypersurfaces. Proc. A.M.S. 105 (1989), 429–435.CrossRefGoogle Scholar