Let γ:x = x(u) for a≤ u ≤ b be a closed curve in n dimensional euclidean space En (for n ≥ 2) referred to some point P0, which does not lie on γ, as origin. We suppose that γ is smooth in the sense that the cartesian coordinates are class C2 functions of the parameter u, and that dx/du is non-vanishing so that a tangent vector is everywhere well defined. These properties are also assumed to hold in an obvious way at the join of the end points u = a and u = b. As P moves on γ its position vector x(u) intersects the surface of the unit sphere centred at P0 in a closed curve γ0. Note that γ0: x = x0(u) may not be smooth everywhere. If there are points P on γ where P0P is tangential to γ at P then dx0/du =0 at the corresponding point on γ0, and γ0 may have a cusp there. We assume that γ0 is smooth except at a finite number of points. We define the total swing of the position vector to γ to be the arc length L0 of γ0. Clearly L0 is not an invariant but depends on the choice of the origin P0 in relation to γ. The total (first) curvature of γ is an invariant and is defined by

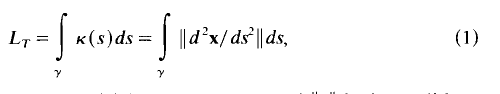
where s is the arc length on γ, K(S) is the curvature and ‖v‖ is the euclidean norm of the vector v. Note that LT is also the arc length of the closed curve γ1, described on a unit sphere by the unit tangent t = dx/ds to γ as position vector, with the centre of the sphere as origin, γ1 is the spherical indicatrix of t. Our purpose is to establish the result

for all choices of P0.