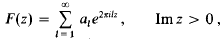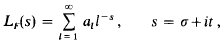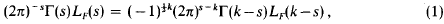Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Good, A.
1984.
Number Theory Noordwijkerhout 1983.
Vol. 1068,
Issue. ,
p.
86.
Good, A.
1985.
Dirichlet and Poincaré series.
Glasgow Mathematical Journal,
Vol. 27,
Issue. ,
p.
39.
Conrey, J. B.
and
Ghosh, A.
1988.
Simple zeros of the Ramanujan ?-Dirichlet series.
Inventiones Mathematicae,
Vol. 94,
Issue. 2,
p.
403.
Duke, W.
1988.
Fourth moments of L‐functions attached to newforms.
Communications on Pure and Applied Mathematics,
Vol. 41,
Issue. 6,
p.
815.
Jutila, M.
1989.
Number Theory.
Vol. 1380,
Issue. ,
p.
120.
HAFNER, JAMES LEE
1989.
Number Theory, Trace Formulas and Discrete Groups.
p.
309.
Ivic, A.
and
Perelli, A.
1990.
Mean values of certain zeta-functions on the critical line.
Lithuanian Mathematical Journal,
Vol. 29,
Issue. 4,
p.
351.
Vinogradov, A. I.
1991.
SLn technique and the density conjecture.
Journal of Soviet Mathematics,
Vol. 53,
Issue. 3,
p.
225.
Fomenko, O. M.
1992.
Distribution of the roots of a quadratic congruence.
Journal of Soviet Mathematics,
Vol. 62,
Issue. 4,
p.
2936.
M�ller, Wolfgang
1992.
The mean square of Dirichlet series associated with automorphic forms.
Monatshefte f�r Mathematik,
Vol. 113,
Issue. 2,
p.
121.
Yogananda, C. S.
1993.
Transformation formula for exponential sums involving fourier coefficients of modular forms.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 103,
Issue. 1,
p.
1.
Iwaniec, H.
and
Sarnak, P.
2000.
Visions in Mathematics.
p.
705.
Matsumoto, Kohji
2000.
Number Theory.
p.
241.
Matsumoto, Kohji
2000.
Number Theory.
p.
241.
Sarnak, Peter
2001.
Estimates for Rankin–Selberg L-Functions and Quantum Unique Ergodicity.
Journal of Functional Analysis,
Vol. 184,
Issue. 2,
p.
419.
Якобсон, Дмитрий
Jakobson, Dmitry
Надирашвили, Николай Семенович
Nadirashvili, Nikolai Semenovich
Тот, Дж
and
Toth, John
2001.
Геометрические свойства собственных функций.
Успехи математических наук,
Vol. 56,
Issue. 6,
p.
67.
Beineke, Jennifer
and
Bump, Daniel
2004.
Moments of the Riemann zeta function and Eisenstein series—II.
Journal of Number Theory,
Vol. 105,
Issue. 1,
p.
175.
Laurin[cbreve]ikas, Antanas
and
Zamarys, Saulius
2005.
Asymptotics for the mean value of normalized zeta-functions of certain cusp forms.
Integral Transforms and Special Functions,
Vol. 16,
Issue. 5-6,
p.
437.
Jutila, Matti
and
Motohashi, Yoichi
2005.
Uniform bound for Hecke L-functions.
Acta Mathematica,
Vol. 195,
Issue. 1,
p.
61.
Jutila, M.
2006.
Sums of the additive divisor problem type and the inner product method.
Journal of Mathematical Sciences,
Vol. 137,
Issue. 2,
p.
4755.