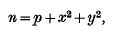Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gallagher, P. X.
1968.
Bombieri's mean value theorem.
Mathematika,
Vol. 15,
Issue. 1,
p.
1.
Orr, Richard C.
1971.
Remainder estimates for squarefree integers in arithmetic progression.
Journal of Number Theory,
Vol. 3,
Issue. 4,
p.
474.
Indlekofer, Karl -Heinz
and
Schwarz, Wolfgang
1972.
�berB-Zwillinge.
Archiv der Mathematik,
Vol. 23,
Issue. 1,
p.
251.
Fujii, Akio
1976.
A local study of some additive problems in the theory of numbers.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 52,
Issue. 3,
Fujii, Akio
1976.
On some analogues of Titchmarsh divisor problem.
Nagoya Mathematical Journal,
Vol. 64,
Issue. ,
p.
149.
Harman, Glyn
1985.
Diophantine approximation with almost‐primes and sums of two squares.
Mathematika,
Vol. 32,
Issue. 2,
p.
301.
Vaughan, R. C.
1998.
Hardy's legacy to number theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 65,
Issue. 2,
p.
238.
Goldston, D. A.
Graham, S. W.
Pintz, J.
and
Yildirim, C. Y.
2010.
Small Gaps Between Almost Primes, the Parity Problem, and Some Conjectures of Erdos on Consecutive Integers.
International Mathematics Research Notices,
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
307.
Elliott, P. D. T. A.
2015.
Additive and multiplicative functions from Nottingham to Urbana-Champaign.
International Journal of Number Theory,
Vol. 11,
Issue. 05,
p.
1357.
Diamond, Harold G.
2017.
Heini Halberstam, 1926-2014.
Bulletin of the London Mathematical Society,
Vol. 49,
Issue. 6,
p.
1119.
Liu, H.-Q.
2017.
An effective Bombieri–Vinogradov theorem and its applications.
Acta Mathematica Hungarica,
Vol. 153,
Issue. 1,
p.
230.
POLLACK, PAUL
2020.
NONNEGATIVE MULTIPLICATIVE FUNCTIONS ON SIFTED SETS, AND THE SQUARE ROOTS OF −1 MODULO SHIFTED PRIMES.
Glasgow Mathematical Journal,
Vol. 62,
Issue. 1,
p.
187.
Assing, Edgar
Blomer, Valentin
and
Li, Junxian
2021.
Uniform Titchmarsh divisor problems.
Advances in Mathematics,
Vol. 393,
Issue. ,
p.
108076.
Gorodetsky, Ofir
and
Grimmelt, Lasse
2024.
On an ErdŐs–Kac-Type Conjecture of Elliott.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 2,
p.
695.