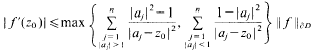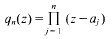Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Xin
1997.
Integral Formulas and Inequalities for Rational Functions.
Journal of Mathematical Analysis and Applications,
Vol. 211,
Issue. 2,
p.
386.
Jones, Roy
Li, Xin
Mohapatra, R.N.
and
Rodriguez, R.S.
1998.
On the Bernstein Inequality for Rational Functions with a Prescribed Zero.
Journal of Approximation Theory,
Vol. 95,
Issue. 3,
p.
476.
Akçay, Hüseyin
2001.
General Orthonormal Bases for Robust Identification in $H_\infty$.
SIAM Journal on Control and Optimization,
Vol. 40,
Issue. 3,
p.
947.
Akçay, Hüseyin
2002.
A stochastic analysis of robust estimation algorithms in H∞ with rational basis functions.
International Journal of Robust and Nonlinear Control,
Vol. 12,
Issue. 1,
p.
71.
Дубинин, Владимир Николаевич
and
Dubinin, Vladimir Nikolaevich
2002.
О применении конформных отображений в неравенствах для рациональных функций.
Известия Российской академии наук. Серия математическая,
Vol. 66,
Issue. 2,
p.
67.
Лукашов, Алексей Леонидович
and
Lukashov, Aleksei Leonidovich
2004.
Неравенства для производных рациональных функций на нескольких отрезках.
Известия Российской академии наук. Серия математическая,
Vol. 68,
Issue. 3,
p.
115.
Baranov, A.D.
2005.
Bernstein-type inequalities for shift-coinvariant subspaces and their applications to Carleson embeddings.
Journal of Functional Analysis,
Vol. 223,
Issue. 1,
p.
116.
Dubinin, V N
and
Kalmykov, S I
2007.
A majoration principle for meromorphic functions.
Sbornik: Mathematics,
Vol. 198,
Issue. 12,
p.
1737.
Дубинин, Владимир Николаевич
Dubinin, Vladimir Nikolaevich
Калмыков, Сергей Иванович
and
Kalmykov, Sergei Ivanovich
2007.
Принцип мажорации для мероморфных функций.
Математический сборник,
Vol. 198,
Issue. 12,
p.
37.
Olesov, A. V.
2010.
Differential inequalities for entire functions of finite degree and rational functions with prescribed poles.
Siberian Mathematical Journal,
Vol. 51,
Issue. 6,
p.
1104.
Qazi, Mohammed A.
and
Rahman, Qazi I.
2010.
Some Estimates for the Derivatives of Rational Functions.
Computational Methods and Function Theory,
Vol. 10,
Issue. 1,
p.
61.
Finis, Tobias
Lapid, Erez
and
Müller, Werner
2011.
On the spectral side of Arthur's trace formula --- absolute convergence.
Annals of Mathematics,
Vol. 174,
Issue. 1,
p.
173.
Дубинин, Владимир Николаевич
and
Dubinin, Vladimir Nikolaevich
2012.
Методы геометрической теории функций в классических и современных задачах для полиномов.
Успехи математических наук,
Vol. 67,
Issue. 4,
p.
3.
İspir, Nurhayat
and
Yıldız Özkan, Esma
2013.
Approximation properties of complex q-Balázs-Szabados operators in compact disks.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Baranov, Anton
and
Zarouf, Rachid
2014.
A model space approach to some classical inequalities for rational functions.
Journal of Mathematical Analysis and Applications,
Vol. 418,
Issue. 1,
p.
121.
Kalmykov, S.I.
and
Nagy, B.
2015.
Polynomial and rational inequalities on analytic Jordan arcs and domains.
Journal of Mathematical Analysis and Applications,
Vol. 430,
Issue. 2,
p.
874.
Qasim, Idrees
and
Liman, A.
2015.
Bernstein type inequalities for rational functions.
Indian Journal of Pure and Applied Mathematics,
Vol. 46,
Issue. 3,
p.
337.
Finis, Tobias
Lapid, Erez
and
Müller, Werner
2015.
LIMIT MULTIPLICITIES FOR PRINCIPAL CONGRUENCE SUBGROUPS OF AND.
Journal of the Institute of Mathematics of Jussieu,
Vol. 14,
Issue. 3,
p.
589.
Müller, Werner
2016.
Families of Automorphic Forms and the Trace Formula.
p.
477.
Li, Xin
Mohapatra, Ram
and
Ranasinghe, Rajitha
2017.
Progress in Approximation Theory and Applicable Complex Analysis.
Vol. 117,
Issue. ,
p.
105.