Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T17:05:06.587Z Has data issue: false hasContentIssue false
  • English
  • Français

The resultant and the Koszul complex of a set of forms

Part of: Ring extensions and related topics

Published online by Cambridge University Press:  26 February 2010

David Kirby
David Kirby
Affiliation:
Faculty of Mathematical Studies, University of Southampton, Highfield, Southampton SO17 IBJ
Get access

Extract

For i = 1,…, n let ai be a homogeneous polynomial of degree ri(>0) in the graded polynomial ring R[x1, …, xm], or R[x] for short, where R is a commutative ring with unity and x1, …, xm are indeterminates of degree 1. Let 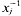of degree - 1 be a formal inverse of xj and let U denote the graded R[x]-module 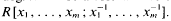In [2, §2] we introduced a graded complex of r-modules.

MSC classification

Secondary: 13B25: Polynomials over commutative rings
Type
Research Article
Information
Mathematika , Volume 44 , Issue 2 , December 1997 , pp. 348 - 356
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Gelfand, I. M.Kapranov, M. M. and Zelevinsky, A. V.. Discriminants, Resultants and Multidimensional Determinants (Birkhäuser, 1994).CrossRefGoogle Scholar
2.Kirby, D.. A sequence of complexes associated with a finite set of homogeneous polynomials. Math. Proc. Camb. Phil. Soc. To appear.Google Scholar
3.Macaulay, F. S.. The algebraic theory of modular systems, Cambridge Tract No. 17 (Cambridge University Press. 1916).CrossRefGoogle Scholar
4.Weyman, J.. Calculating discrimin ants by higher direct images. Trans. Amer. Math. Soc., 343 (1994), 367–389.CrossRefGoogle Scholar
5.Weyman, J. and Zelevinsky, A. V.. Determinanlal formulas for multigraded resultanls. J. Alg. Geom., 3 (1994), 569597.Google Scholar