Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-26T16:22:32.614Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on Siegel's theorem on algebraic curves

Published online by Cambridge University Press:  26 February 2010

K. Mahler
K. Mahler
Affiliation:
Department of Mathematics, University of Manchester, Manchester, 13.
Get access

Extract

The main case of Siegel's theorem on algebraic curves may be stated as follows:

THEOREM 1. Let

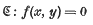
be an irreducible algebraic curve of genus g≥1, ƒ(x, y) being a polynomial with algebraic coefficients. Let K be an algebraic field of finite degree over the rational field; let o be the ring of integers in K; and let j be a positive rational integer. Then there are at most finitely many points (x, y) on ℭ for which jxεο and yεK.

Type
Research Article
Information
Mathematika , Volume 2 , Issue 2 , December 1955 , pp. 116 - 127
Copyright
Copyright © University College London 1955

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 116 note * Siegel, C. L., Abh. Preuss. Akad. Wiss. (1920), No. 1Google Scholar.

page 116 note † An analogous theorem holds in which the coefficients of ƒ(x, y) and the elements of the two moduli X and Y are p-adic numbers or, more generally, p-adic numbers.

page 117 note * Proc. London Math. Soc. (2), 47 (1942), 351–403Google Scholar, in particular p. 363.

page 127 note * I wish to express my thanks to D. G. Northcott for reading my manuscript and noticing an error in my original proof of Lemma 1, and to B. Segre for giving the reference to his paper of 1942 which allowed me to correct this error.