Article contents
Projecting and uniformising Borel sets with 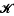 σ, sections I.
σ, sections I.
Published online by Cambridge University Press: 26 February 2010
Extract
Introduction. Suppose that M i s a set in a cartesian product space X × Y. If X and Y are both R1 and M is a borel set, K. Kunugui [1] and W. J. Arsenin [2] have shown that those points which lie on sections {x} × Y which meet M in a nonempty Kσ set project onto a set in X which is the complement of an analytic set. Somewhat later, W. J. Arsenin and A. A. Lyapunov [3] reproduced the proof from [2], still apparently without being aware of Kunugui's results. Although, as we shall see later, Kunugui's proof seems to be incorrect, it does contain an ingenious lemma (Lemma 5 below). Actually [2] also contains this lemma in a disguised form that seems, to me at least, to be less satisfactory. One of the purposes of this article is to give a promised proof, see D. G. Larman [4] of Kunugui's theorem in slightly more general circumstances by combining ideas of Kunugui [1] with those of P. Novikoflf [5].
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1972
- 8
- Cited by


