Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Swan, Richard G
1971.
Generators and relations for certain special linear groups.
Advances in Mathematics,
Vol. 6,
Issue. 1,
p.
1.
Merzlyakov, Yu. I.
1973.
Linear groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
571.
1974.
Noneuclidean Tesselations and Their Groups.
Vol. 61,
Issue. ,
p.
199.
Behr, Helmut
1975.
Explizite Pr�sentation von Chevalleygruppen �ber ?.
Mathematische Zeitschrift,
Vol. 141,
Issue. 3,
p.
235.
Fine, Benjamin
1975.
The HNN and generalized free product structure of certain linear groups.
Bulletin of the American Mathematical Society,
Vol. 81,
Issue. 2,
p.
413.
Hurrelbrink, J�rgen
and
Rehmann, Ulf
1976.
Zur endlichen Pr�sentation von Chevalley-Gruppen �ber den euklidischen imagin�r-quadratischen Zahlringen.
Archiv der Mathematik,
Vol. 27,
Issue. 1,
p.
123.
Menal, Pere
1979.
Remarks on the GL2 of a ring.
Journal of Algebra,
Vol. 61,
Issue. 2,
p.
335.
Fine, Benjamin
1990.
The euclidean bianchi group.
Communications in Algebra,
Vol. 18,
Issue. 8,
p.
2461.
Morita, Jun
1995.
The group SL(2,Zs) is either perfect or prosolvable.
Communications in Algebra,
Vol. 23,
Issue. 9,
p.
3545.
Hazewinkel, M.
1997.
Encyclopaedia of Mathematics.
p.
71.
Bardini, Carla
and
Chen, Yu
2006.
Homomorphisms of two-dimensional linear groups over a ring of stable range one.
Journal of Algebra,
Vol. 303,
Issue. 1,
p.
30.
Mushtaq, Qaiser
and
Asif, Shehla
2010.
A5as a Homomorphic Image of a Subgroup of Picard Group.
Communications in Algebra,
Vol. 38,
Issue. 10,
p.
3897.
Bogdan Nica
2011.
The Unreasonable Slightness of E<sub>2</sub> over Imaginary Quadratic Rings.
The American Mathematical Monthly,
Vol. 118,
Issue. 5,
p.
455.
Mushtaq, Qaiser
and
Asif, Shahla
2012.
Finite permutation representation of a subgroup of picard group.
Acta Mathematica Scientia,
Vol. 32,
Issue. 3,
p.
842.
Vavilov, N. A.
and
Stepanov, A. V.
2013.
Linear groups over general rings. I. Generalities.
Journal of Mathematical Sciences,
Vol. 188,
Issue. 5,
p.
490.
Boylan, Hatice
and
Skoruppa, Nils-Peter
2013.
Linear characters of SL2 over Dedekind domains.
Journal of Algebra,
Vol. 373,
Issue. ,
p.
120.
Şengün, Mehmet Haluk
2014.
Computations with Modular Forms.
Vol. 6,
Issue. ,
p.
279.
Sin, Peter
and
Thompson, John G.
2014.
Some uniserial representations of certain special linear groups.
Journal of Algebra,
Vol. 398,
Issue. ,
p.
448.
Xie, BaoHua
Wang, JieYan
and
Jiang, YuePing
2015.
Generators of the Gauss–Picard modular group in three complex dimensions.
Pacific Journal of Mathematics,
Vol. 273,
Issue. 1,
p.
197.
Prasad, Gopal
and
Rapinchuk, Andrei S.
2016.
On the congruence kernel for simple algebraic groups.
Proceedings of the Steklov Institute of Mathematics,
Vol. 292,
Issue. 1,
p.
216.
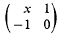 as x ranges over R; the structure of E2(R)a has been described in a recent theorem [2; Th. 9.3] for certain rings R, the “quasi-free rings for GE2” (cf. §2 below). Now over a commutative Euclidean domain, E2(R) is just the special linear group SL2(R); this suggests applying the theorem to the ring of integers in a Euclidean number field. However, the only number fields whose rings were shown to be quasi-free for GE2 in [2] were the non-Euclidean imaginary quadratic fields. In fact that leaves the application of Th. 9.3 of [2] to the ring of Gaussian integers unjustified (I am indebted to J.-P. Serre for drawing this oversight to my attention). In order to justify this application one would have to show either (a) that the Gaussian integers are quasi-free for GE2., or (b) that Th. 9.3 of [2] holds under weaker hypotheses which are satisfied by the Gaussian integers. Our object in this note is to establish (b)–indeed our only course, since the Gaussian integers turn out to be not quasi-free.
as x ranges over R; the structure of E2(R)a has been described in a recent theorem [2; Th. 9.3] for certain rings R, the “quasi-free rings for GE2” (cf. §2 below). Now over a commutative Euclidean domain, E2(R) is just the special linear group SL2(R); this suggests applying the theorem to the ring of integers in a Euclidean number field. However, the only number fields whose rings were shown to be quasi-free for GE2 in [2] were the non-Euclidean imaginary quadratic fields. In fact that leaves the application of Th. 9.3 of [2] to the ring of Gaussian integers unjustified (I am indebted to J.-P. Serre for drawing this oversight to my attention). In order to justify this application one would have to show either (a) that the Gaussian integers are quasi-free for GE2., or (b) that Th. 9.3 of [2] holds under weaker hypotheses which are satisfied by the Gaussian integers. Our object in this note is to establish (b)–indeed our only course, since the Gaussian integers turn out to be not quasi-free.