Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T14:52:55.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Positive values of indefinite quadratic forms

Published online by Cambridge University Press:  26 February 2010

R. J. Cook  and
S. Raghavan
R. J. Cook
Affiliation:
Department of Pure Mathematics, University of Sheffield, Western Bank, Sheffield S10 2TN.
S. Raghavan
Affiliation:
Department of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400 005, India.
Get access

Extract

Let

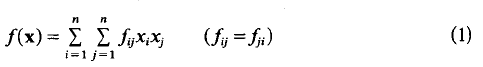
be a real quadratic form in n variables with integral coefficients (i.e., 2fij ε ℤ, fiiε ℤ.) and determinant D ≠ O. A well-known theorem of Cassels [1] states that if the equation f = 0 is properly soluble in integers x1 … , xn then there is a solution satisfying

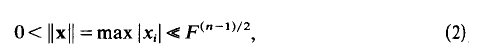
where F = max |fij and we use the «-notation with an implicit factor depending only on n. More recently it has been shown that f has n linearly independent zeros x1 …, xn satisfying

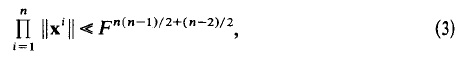
(see [2, 3 and 6])

Type
Research Article
Information
Mathematika , Volume 33 , Issue 1 , June 1986 , pp. 164 - 169
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Cassels, J. W. S.. Bounds for the least solutions of homogeneous quadratic equations. Proc. Camb. Phil Soc, 51 (1955), 262–264; Addendum, Proc. Camb. Phil Soc, 52 (1956), 604.CrossRefGoogle Scholar
2.Cook, R. J. and Raghavan, S.. Small independent zeros of quadratic forms. To appear.Google Scholar
3.Davenport, H.. Homogeneous quadratic equations. Mathematika, 18 (1971), 1–4.CrossRefGoogle Scholar
4.Lawton, B.. Bounded representations of the positive values of an indefinite quadratic form. Proc Camb. Phil. Soc, 54 (1958), 14–17.CrossRefGoogle Scholar
5.Mirsky, L.. Introduction to linear algebra (Oxford, 1955), reprinted by Paperbacks, Dover, New York, 1982.Google Scholar
6.Schulze-Pillot, R.. Small linearly independent zeros of quadratic forms. Monatsh. Math., 95 (1983), 241–249.CrossRefGoogle Scholar
7.Watson, G. L.. Least solutions of homogeneous quadratic equations. Proc. Camb. Phil. Soc, 53 (1957), 541–543.Google Scholar