Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T17:03:42.178Z Has data issue: false hasContentIssue false
  • English
  • Français

On uniqueness of flows for a class of second-order fluids

Published online by Cambridge University Press:  26 February 2010

R. N. Hills
R. N. Hills
Affiliation:
School of Mathematics, The University of Newcastle upon Tyne, Newcastle upon Tyne.
Get access

Extract

In the present paper we consider the uniqueness of the solutions of the equations governing the motion of an incompressible second-order fluid in a bounded region. For such a fluid model the stress tensor S in a rectangular Cartesian coordinate system xi at a point xi of the fluid is determined from

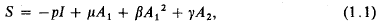
where I is the unit tensor, p the hydrostatic pressure and μ, β, γ are material constants. The tensors A1 and A2 are the first and second Rivlin-Ericksen tensors which are defined in terms of the velocity field vi by

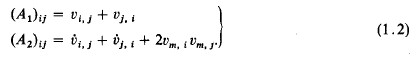
Type
Research Article
Information
Mathematika , Volume 17 , Issue 2 , December 1970 , pp. 333 - 337
Copyright
Copyright © University College London 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Coleman, B. D. and Noll, W., Arch. Rat. Mech. Anal., 6 (1960), 355.CrossRefGoogle Scholar
2.Rivlin, R. S. and Ericksen, J. L., J. Rat. Mech. Anal., 4 (1955), 323.Google Scholar
3.Ting, T. W., Arch. Rat. Mech. Anal., 14 (1963), 1.CrossRefGoogle Scholar
4.Coleman, B. D., Duffin, R. J. and Mizel, V. J., Arch. Rat. Mech. Anal., 19 (1965), 100.CrossRefGoogle Scholar
5.Fosdick, R. L. and Bernstein, B., Int. J. Eng. Sci., 7 (1969), 555.CrossRefGoogle Scholar
6.Coleman, B. D. and Markovitz, H., J. App. Phys., 35 (1964), 1.CrossRefGoogle Scholar
7.Coleman, B. D. and Markovitz, H. and Noll, W., Arch. Rat. Mech. Anal., 13 (1963), 167.Google Scholar
8.Green, A. E. and Laws, N., Quart. J. Mech. App. Math., 20 (1967), 265.CrossRefGoogle Scholar
9.Serrin, J., Handbuch der Physik Vol. VIII/1 Edited by S. Flügge and C. Truesdell (Springer-Verlag, 1959).Google Scholar