Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T16:40:29.402Z Has data issue: false hasContentIssue false
  • English
  • Français

On the length of faithful nuclear representations of finite rank operators

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  26 February 2010

A. Pełczynski  and
Nicole Tomczak-Jaegermann
A. Pełczynski
Affiliation:
Institut of Mathematics, Polish Academy of Sciences, Sniadeckich 8, 00-950 Warsaw, Poland.
Nicole Tomczak-Jaegermann
Affiliation:
Department of Mathematics, University of Alberta, Edmonton, Alberta, Canada, T6G 2G1.
Get access

Abstract

We study the minimal length of faithful nuclear representations of operators acting between finite-dimensional Banach spaces and the related minimal number of contact points of the John ellipsoid of maximal volume contained in the unit ball of a finite-dimensional Banach space. In both cases the classical upper estimates, which follow from the Caratheodory theorem, are shown to be exact. Related isometric characterizations of 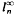are proved.

MSC classification

Secondary: 46B20: Geometry and structure of normed linear spaces
Type
Research Article
Information
Mathematika , Volume 35 , Issue 1 , June 1988 , pp. 126 - 143
Copyright
Copyright © University College London 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

DGK.Danzer, L., Grünbaum, B., and Klee, V.. Helly's theorem and relatives. Proc. Symp. Pure Math. Vol. 7, Convexity (Providence, 1963), 101–180.Google Scholar
DSch.Dunford, N. and Schwarz, J.. Linear Operators (Interscience, 1958).Google Scholar
J.John, F.. Extremum problems with inequalities as subsidiary conditions. Courant Anniversary Volume (Interscience, 1948), 187–204.Google Scholar
K.König, H.. Spaces with large projection constants. Israel J. Math., 50(1985), 181–188.Google Scholar
KZ.Kaczynski, T. and Zeidan, V.. An application of Ky-Fan fixed point theorem to an optimization problem. To appear in the j Non-linear Analysis.Google Scholar
L.Lewis, D. R.. Ellipsoids defined by Banach ideal norms. Mathematika, 26(1979), 18–29.Google Scholar
N.Nachbin, L.. A theorem of the Hahn-Banach type for linear transformations. Trans. Amer. Math. Soc, 68(1950), 28–46.Google Scholar
P.Pelczynski, A.. Geometry of finite-dimensional Banach Spaces and Operator Ideals; in Notes in Banach Spaces (Austin University Press, 1980), 81–181.Google Scholar
T-JTomczak-Jaegermann, N.. Banach-Mazur Distances and Finite-Dimensional Operators Ideals. To appear (Longman, 1988).Google Scholar