Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T21:16:21.570Z Has data issue: false hasContentIssue false
  • English
  • Français

On the frequency distribution of partial quotients of U-numbers

Part of: Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  26 February 2010

Edward B. Burger  and
Thomas Struppeck
Edward B. Burger
Affiliation:
Department of Mathematics, Williams College, Williamstown, Mass. 01267, U.S.A.
Thomas Struppeck
Affiliation:
Department of Mathematics, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
Get access

Extract

In Mahler's classification of complex numbers [10] (see [4]), a transcendental number ξ is called a U-number if there exists a fixed integer N ≥ 1 so that for all ω > 0, there exists a polynomial 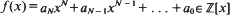so that

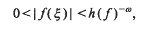
where the height h(f) = max {|α0|, |α1|, …, |αN|}. The number ξ is called a Um-number if the above holds for N = m but for no smaller value of N (examples and further details may be found in [9,1 and 2]). Thus the set of U1-numbers is precisely the set of Liouville numbers. In this paper we investigate the statistical behavior of the partial quotients of real U-numbers, in particular, U2-numbers. In addition, we demonstrate the existence of a U2-number with the property that if it is translated by any nonnegative integer and then squared, the result is a Liouville number. Related results involving badly approximate U2-numbers are also discussed.

MSC classification

Secondary: 11J82: Measures of irrationality and of transcendence
Type
Research Article
Information
Mathematika , Volume 40 , Issue 2 , December 1993 , pp. 215 - 225
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Alniacik, K.. On Mahler's U-numbers. Amer. J. of Math., 105 (1983), 1347–1356.CrossRefGoogle Scholar
2.Alniacik, K.. Representation of real numbers as sums of U2-numbers. Acta Arith., 55 (1990), 301–310.CrossRefGoogle Scholar
3.Baker, A.. Continued fractions of transcendental numbers. Mathematika, 9 (1962), 1–8.Google Scholar
4.Baker, A.. Transcendental Number Theory (Cambridge and London, Cambridge University Press, 1979).Google Scholar
5.Davenport, H.. A note on Diophantine approximation (II). Mathematika, 11 (1964), 50–58.CrossRefGoogle Scholar
6.Erdős, P.. Representations of real numbers as sums and products of Liouville numbers. Michigan Math. J., (1962), 59–60.CrossRefGoogle Scholar
7.Khinchin, A. Ya.. Continued Fractions (Chicago and London, The University of Chicago Press, 1964).Google Scholar
8.LeVeque, W. J.. Fundamentals of Number Theory (Reading and Menlo Park, Addison-Wesley, 1977).Google Scholar
9.LeVeque, W. J.. On Mahler's U-numbers. J. London Math. Soc., 28 (1953), 220–229.CrossRefGoogle Scholar
10.Mahler, K.. Zur Approximation der Exponentialfunktion und des Logarithmus, I. J. reine agnew. Math., 166 (1932), 118–136.Google Scholar
11.Maillet, E.. Introduction à la thèorie des nombres transcendants et les propriétés arithmétiques des fonctions (Paris, Gauthier-Villars, 1906).Google Scholar
12.van der Poorten, A. J.. An introduction to continued fractions. Diophantine Analysis, Loxton, J. H. and van der Poorten, A. J., eds., London Math. Soc. Lecture Note Series, 109 (Cambridge University Press, 1986).Google Scholar
13.van der Poorten, A. J., Fractions of the period of the continued fraction expansinon of quadratic integers. Bull. Austral. Math. Soc., 44 (1991), 155–169.Google Scholar