Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-06T10:17:35.162Z Has data issue: false hasContentIssue false
  • English
  • Français

On the fractional parts of a set of points

Published online by Cambridge University Press:  26 February 2010

R. J. Cook
R. J. Cook
Affiliation:
University College, Cardiff
Get access

Extract

Heilbronn [5] proved that for any ε > 0 there exists C(ε) such that for any real θ and N ≥ 1 there is an integer x satisfying

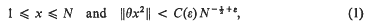
where ‖α‖ denotes the difference between α and the nearest integer, taken positively. The result is uniform in θ and so analogous to Dirichlet's inequality for the fractional parts of nθ. The result has been generalized to simultaneous approximations by Danicic [1] and Ming-chit Liu [6]. Here we shall extend the result to any finite number of simultaneous approximations when x2 is replaced by a k-th power.

Type
Research Article
Information
Mathematika , Volume 19 , Issue 1 , June 1972 , pp. 63 - 68
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Danicic, I., “On the fractional parts of θx2 and φx2”, J. London Math. Soc., 34 (1959), 353–357.CrossRefGoogle Scholar
2.Davenport, H., Analytic methods for Diophantine equations and Diophantine inequalities (Ann Arbor, Michigan, 1962).Google Scholar
3.Davenport, H., “On a theorem of Heilbronn”, Quart. J. Math. Oxford (2), 18 (1967), 339–344.CrossRefGoogle Scholar
4.Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (Oxford University Press, 4th ed., 1965).Google Scholar
5.Heilbronn, H., “On the distribution of the sequence n 2θ (mod 1)”, Quart. J. Math. Oxford, 19 (1948), 249–256.CrossRefGoogle Scholar
6.Liu, Ming-chit, “On the fractional parts of θnk and φn k”, Quart. J. Math. Oxford (2), 21 (1970), 481–486.CrossRefGoogle Scholar
7.Vinogradov, I. M., The method of trigonometrical sums in the theory of numbers, (translated by Roth, K. F. and Davenport, Anne) (Interscience Publishers, 1954).Google Scholar