Truesdell and Noll [1; sections 22, 27, 34] have discussed the concepts of material uniformity and homogeneity in continuum mechanics. A body is said to be materially uniform if, roughly speaking, all the particles composing the body are of the same material and homogeneous if there exists a global reference configuration which can be taken as a natural state for the whole body. To make the ideas precise for elastic materials, consider a small neighbourhood 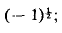of each particle X and suppose that a reference configuration κ is chosen for each 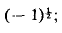. Then during the motion, the deformation gradients may be calculated at each point X relative to the local reference configurations k. The stress at X is a function of these deformation gradients and if the stress relation does not depend explicitly on X the body is said to be materially uniform. If each local reference configuration κ can be taken as the configuration of its associated set of particles 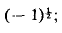in some global reference configuration for the whole body, the body is said to be homogeneous. In general, however, the configurations κ need not fit together to form a global reference configuration. The body is then said to contain a distribution of dislocations.