Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ullom, S.
1970.
A note on the classgroup of integral group rings of some cyclic groups.
Mathematika,
Vol. 17,
Issue. 1,
p.
79.
Fröhlich, A.
1972.
On the classgroup of integral grouprings of finite Abelian groups II.
Mathematika,
Vol. 19,
Issue. 1,
p.
51.
Galovich, S.
Reiner, I.
and
Ullom, S.
1972.
Class groups for integral representations of metacyclic groups.
Mathematika,
Vol. 19,
Issue. 1,
p.
105.
Reiner, I.
and
Ullom, S.
1973.
Proceedings of the Conference on Orders, Group Rings and Related Topics.
Vol. 353,
Issue. ,
p.
139.
Plotkin, B. I.
1973.
General theory of groups.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
527.
Fröhlich, A.
1973.
The Picard group of noncommutative rings, in particular of orders.
Transactions of the American Mathematical Society,
Vol. 180,
Issue. 0,
p.
1.
Reiner, I
and
Ullom, S
1974.
A Mayer-Vietoris sequence for class groups.
Journal of Algebra,
Vol. 31,
Issue. 2,
p.
305.
Fröhlich, A.
Keating, M. E.
and
Wilson, S. M. J.
1974.
The class groups of quaternion and dihedral 2‐groups.
Mathematika,
Vol. 21,
Issue. 1,
p.
64.
Galovich, Steven
1974.
The class group of a cyclic p-group.
Journal of Algebra,
Vol. 30,
Issue. 1-3,
p.
368.
Ullom, Stephen V
1974.
The exponent of class groups.
Journal of Algebra,
Vol. 29,
Issue. 1,
p.
124.
Reiner, Irving
1975.
Representations of Algebras.
Vol. 488,
Issue. ,
p.
253.
Cassou-Noguès, Philippe
1976.
Groupe des classes de l'algèbre d'un groupe métacyclique.
Journal of Algebra,
Vol. 41,
Issue. 1,
p.
116.
Gustafson, William H.
1976.
Brauer Groups.
Vol. 549,
Issue. ,
p.
92.
Kervaire, Michel A.
and
Murthy, M. Pavaman
1977.
On the projective class group of cyclic groups of prime power order.
Commentarii Mathematici Helvetici,
Vol. 52,
Issue. 1,
p.
415.
Ullom, Stephen V
1977.
Fine structure of class groups of cyclic p-groups.
Journal of Algebra,
Vol. 49,
Issue. 1,
p.
112.
Mislin, Guido
1980.
The geometric realization of Wall obstructions by nilpotent and simple spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 87,
Issue. 2,
p.
199.
McCulloh, Leon R.
1981.
A class number formula for elementary-abelian-group rings.
Journal of Algebra,
Vol. 68,
Issue. 2,
p.
443.
Endo, Shizuo
Miyata, Takehiko
and
Sekiguchi, Katsusuke
1982.
Picard groups and automorphism groups of integral group rings of metacyclic groups.
Journal of Algebra,
Vol. 77,
Issue. 2,
p.
286.
Oliver, Robert
1983.
D(ℤπ)+ and the artin cokernel.
Commentarii Mathematici Helvetici,
Vol. 58,
Issue. 1,
p.
291.
Milgram, R. James
1985.
Algebraic and Geometric Topology.
Vol. 1126,
Issue. ,
p.
127.
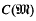 of the maximal order
of the maximal order 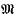 in the rational groupring Q(Γ). Now
in the rational groupring Q(Γ). Now 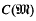 is known in the sense that it is the product of the classgroups of the algebraic integer rings, whose quotient fields appear in the decomposition of Q(Γ). One is thus also interested in the kernel D(Z(Γ)) of the map
is known in the sense that it is the product of the classgroups of the algebraic integer rings, whose quotient fields appear in the decomposition of Q(Γ). One is thus also interested in the kernel D(Z(Γ)) of the map 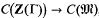 , and it is this which concerns us here. I shall show that it can become very big.
, and it is this which concerns us here. I shall show that it can become very big.

