Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-06T10:16:49.980Z Has data issue: false hasContentIssue false
  • English
  • Français

On some solutions of the Falkner-Skan equation

Part of: Incompressible viscous fluids Boundary value problems

Published online by Cambridge University Press:  26 February 2010

S. P. Hastings  and
S. Siegel
S. P. Hastings
Affiliation:
State University of New York at Buffalo, Buffalo, N.Y., U.S.A.
S. Siegel
Affiliation:
Niagara University.
Get access

Extract

We shall be concerned with two boundary value problems for the Falkner-Skan Equation

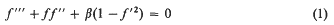
when –β is a small positive number. Our interest is in solutions of (1) which exhibit “reversed flow”; that is, solutions f such that f′(x) < 0 for small positive values of x. The boundary conditions which we wish to consider are

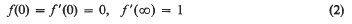
and

MSC classification

Secondary: 34B30: Special equations (Mathieu, Hill, Bessel, etc.) 76D10: Boundary-layer theory, separation and reattachment, higher-order effects
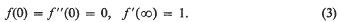
Type
Research Article
Information
Mathematika , Volume 19 , Issue 1 , June 1972 , pp. 76 - 83
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Chapman, D. R., “A theoretical analysis of heat transfer in regions of separated flow”, Nat. Adv. Comm. Aero. Tech. Note, 3792 (1956).Google Scholar
2.Coppel, W. A., “On a differential equation of boundary-layer theory”, Phil. Trans. Royal Soc., 253(1960), 101–136.Google Scholar
3.Hartman, P., “On the asymptotic behavior of solutions of a differential equation in boundary layer theory”, Z. Angew. Math. Mech., 44 (1964), 123–128.Google Scholar
4.Hartman, P., Ordinary Differential Equations (Wiley, New York, 1964).Google Scholar
5.Hartman, P.“On the existence of similar solutions of some boundary layer problems”, SIAMJ. Math. Anal., 3 (1972), 120–147.Google Scholar
6.Hastings, S. P., “Reversed flow solutions of the Falkner-Skan equation”, to appear in SIAM Journal of Applied Math., 22 (1972), 329–334.Google Scholar
7.Kennedy, E. D., “Wake-like solutions of the boundary layer equations”, Amer. Inst. Aero. Astro. Journal, 2 (1964), 225–231.Google Scholar
8.Stewartson, K., “Further solutions of the Falkner-Skan equation”, Proc. Cambridge Phil. Soc., 50 (1954), 454–465.Google Scholar
9.Stewartson, K., “Falkner-Skan equation for wakes”, Amer. Inst. Aero. Astro. Journal, 2 (1964), 1327–1328.Google Scholar
10.Brown, S. N. and Stewartson, K., “On the reversed flow solutions of the Falkner-Skan equation”, Mathematika, 13 (1966), 1–6.Google Scholar