No CrossRef data available.
Article contents
On simultaneous diagonal inequalities, II
Published online by Cambridge University Press: 26 February 2010
Extract
In this paper we continue the investigation begun in [11]. Let λ1…., λs and μ1, …, μs be real numbers, and define the forms
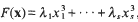
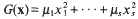
Further, let τ be a positive real number. Our goal is to determine conditions under which the system of inequalities
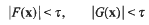
has a non-trivial integral solution. As has frequently been the case in work on systems of diophantine inequalities (see, for example, Brüdern and Cook [6] and Cook [7]), we were forced in [11] to impose a condition requiring certain coefficient ratios to be algebraic. A recent paper of Bentkus and Gotze [4] introduced a method for avoiding such a restriction in the study of positivede finite quadratic forms, and these ideas are in fact flexible enough to be applied to other problems. In particular, Freeman [10] was able to adapt the method to obtain an asymptotic lower bound for the number of solutions of a single diophantine inequality, thus finally providing the expected strengthening of a classical theorem of Davenport and Heilbronn [9]. The purpose of the present note is to apply these new ideas to the system of inequalities (1.1).
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2001


